Volejte
+ 420 603 40 77 11

Systémová dynamika
Zda je pro úspěch systémově dynamických projektů nutná kvalitativní fáze, v níž je vytvářen příčinný smyčkový diagram (CLD) je stále předmětem diskusí. Po téměř třiceti letech zkušeností považujeme diagram za conditio sine qua non úspěchu a do projektů bez diagramu, který vyjadřuje základní zpětnovazební strukturu a vztahy, se nepouštíme.
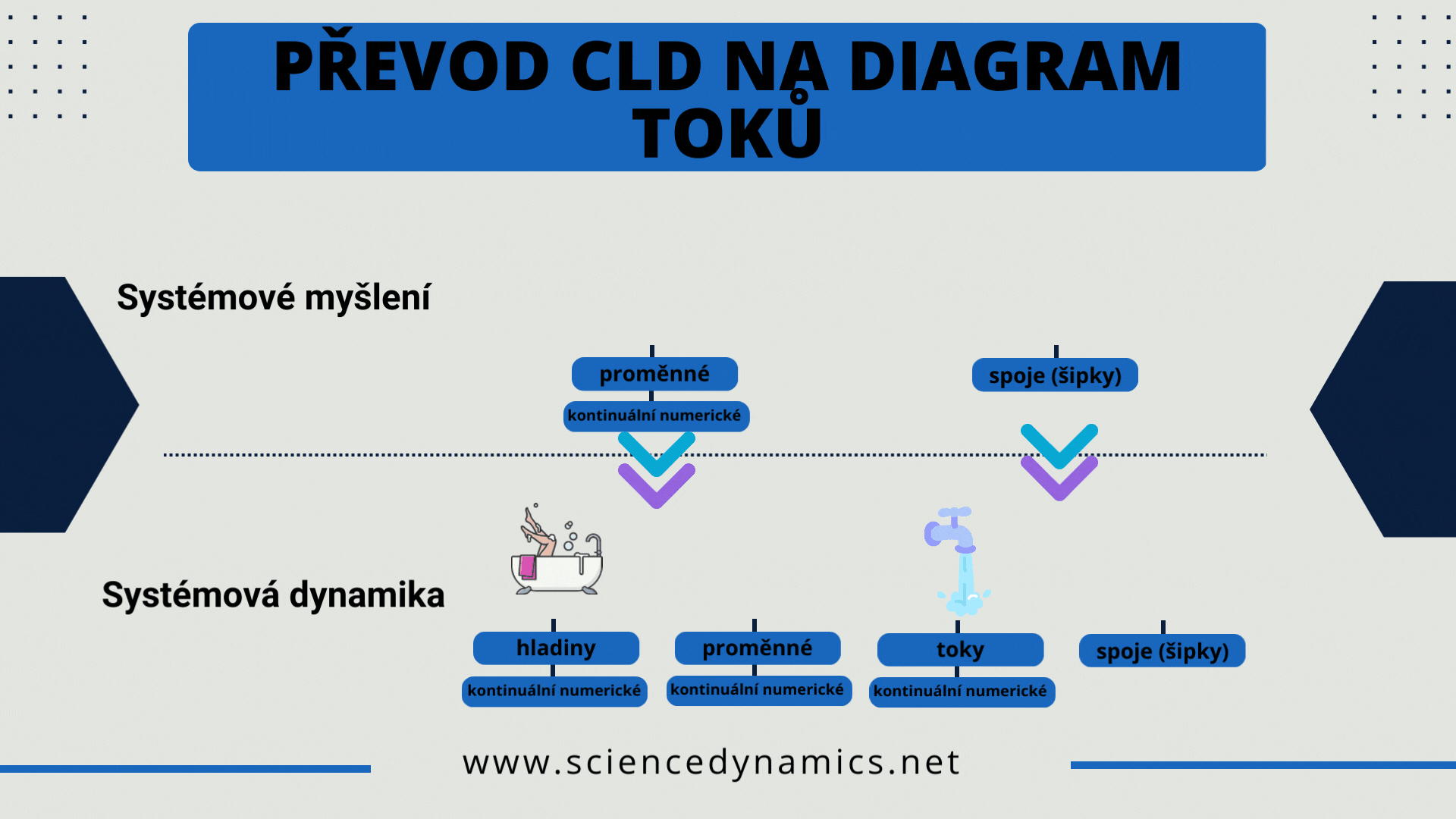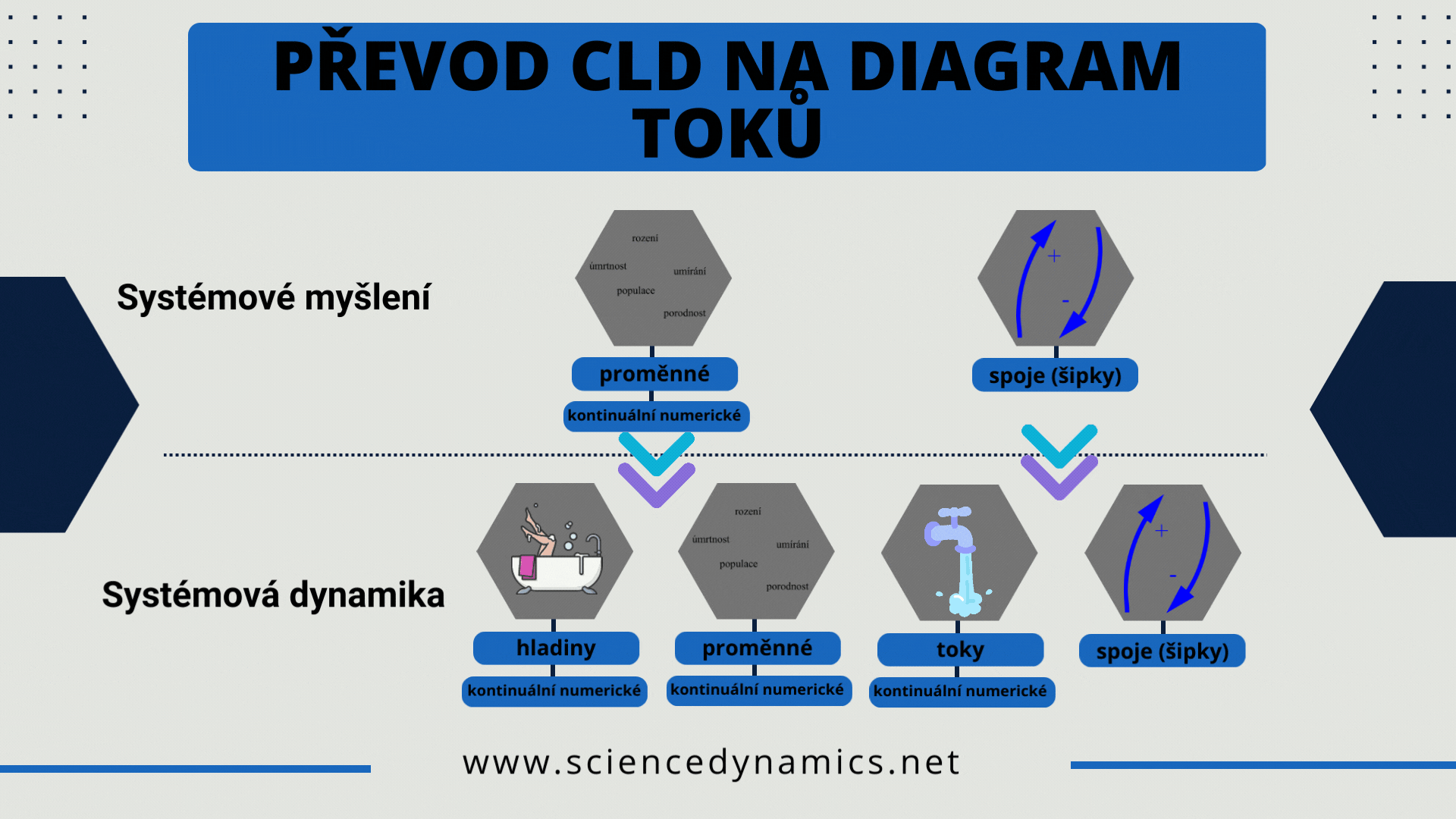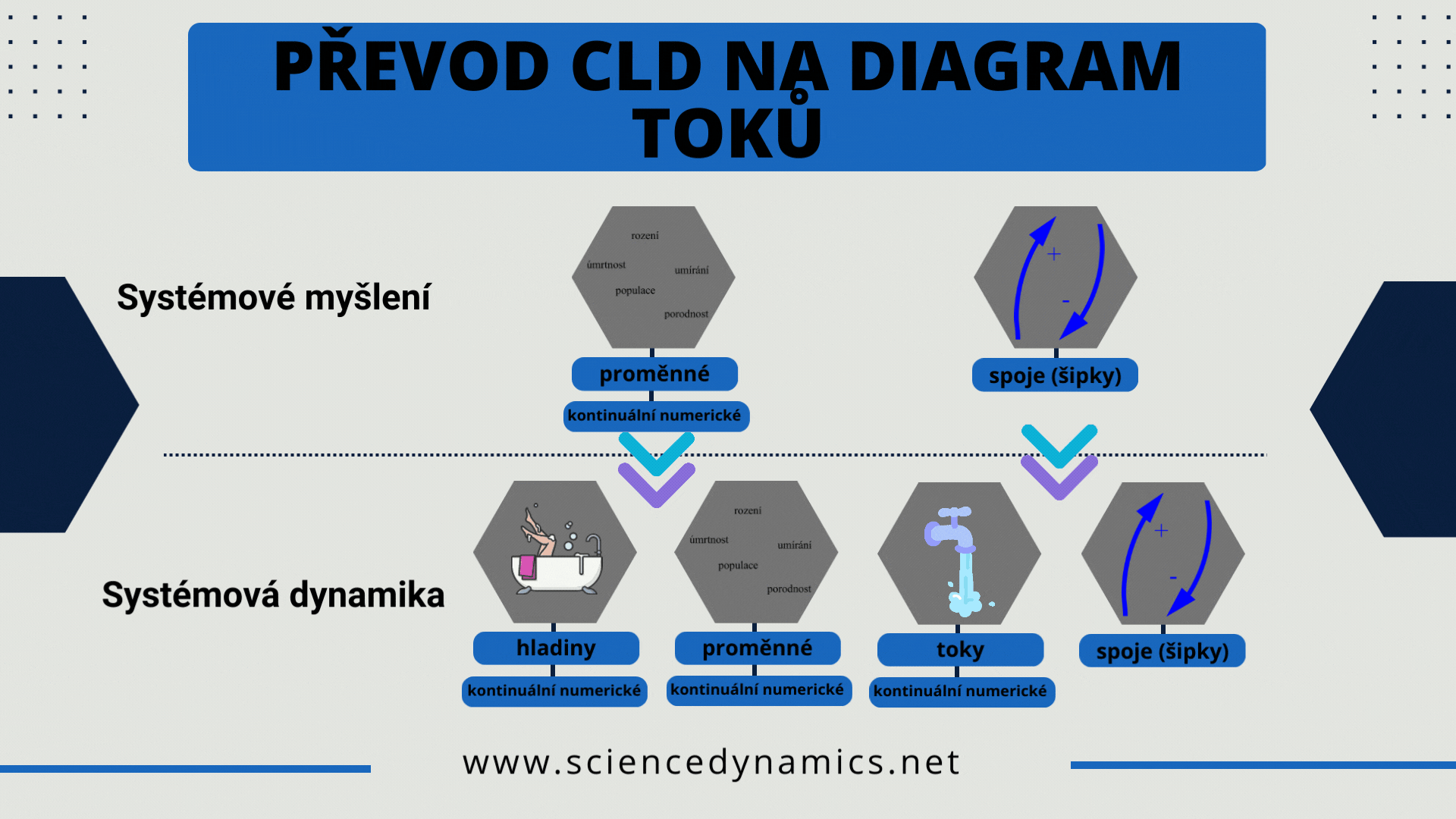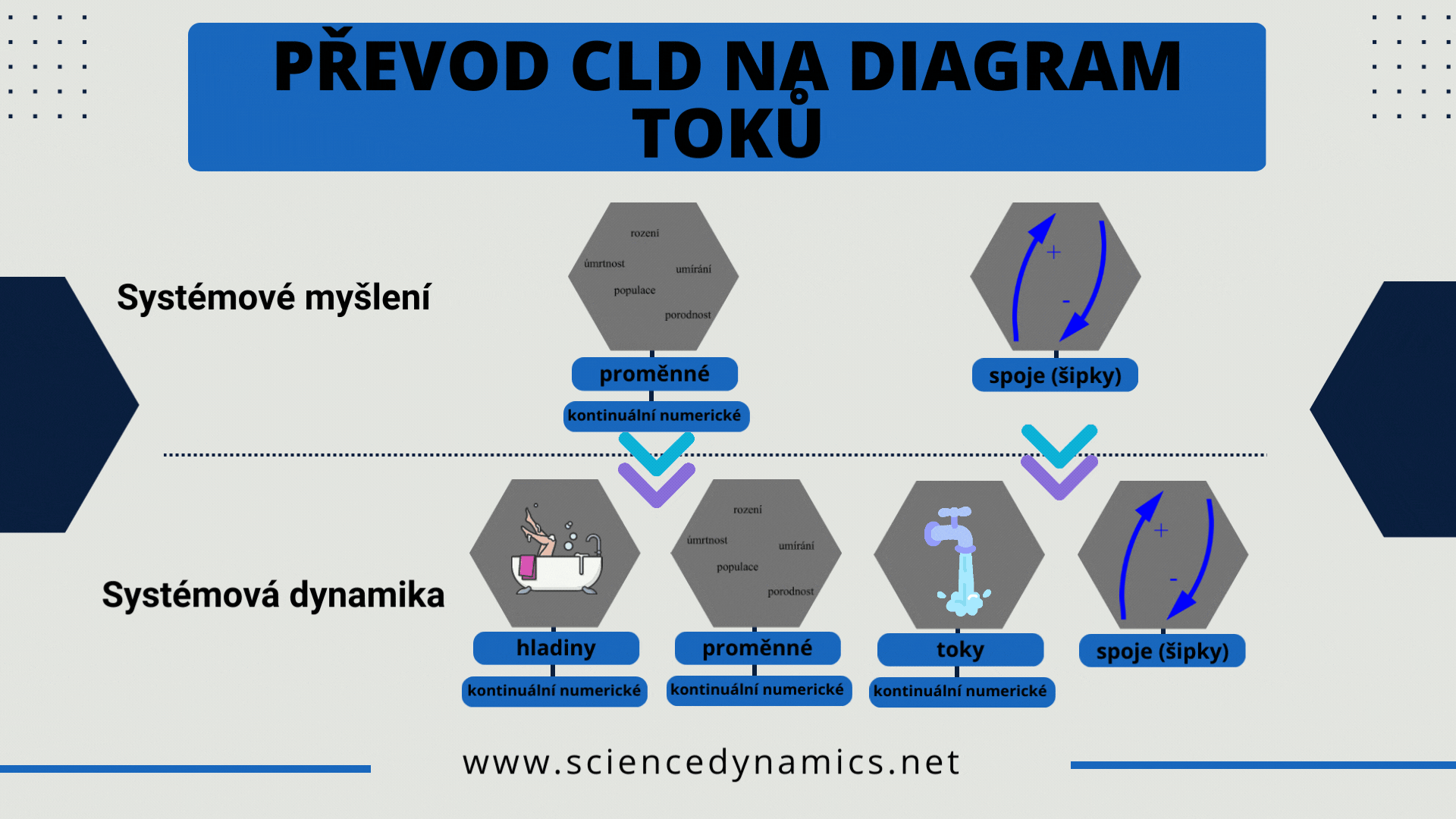
Máme-li diagram hotový, lze se přesunout z domény systémového myšlení do oblasti systémové dynamiky a čeká nás fáze převodu příčinného smyčkového diagramu na tzv. diagram hladin a toků (zkráceně diagram toků - flow diagram - FD). V článku věnovaném systémovému myšlení jsme psali, že jeho klíčový nástroj - příčinný smyčkový diagram - pracuje se dvěma typy prvků - proměnnými a šipkami (spoji).
Obrázek 1 Pravidla pro převod příčinného smyčkového diagramu na diagram toků.
Úlohou systémové dynamiky je matematizovat CLD, převést diagram do počítačem simulovatelné podoby, protože mentální simulace složitějšího CLD není možná. Dva prvky CLD však k matematickému vyjádření struktury systému nestačí. Jsou zapotřebí čtyři. Tokový, počítačově simulovatelný diagram vyžaduje správné přiřazení prvků CLD k prvkům FD. Možnosti jsou popsány na obrázku 1.
Základní premisou systémové dynamiky je, že k dynamickému chování dochází při akumulaci toků v hladinách. Lze tedy říci, že pokud nedochází k akumulaci toků v hladinách, nelze o dynamickém chování hovořit. Klíčovým prvkem každého dynamického modelu je tedy hladina (nazývaná také " stav" nebo "akumulace"). Jak bylo uvedeno v předchozím odstavci, účelem systémové dynamiky je matematicky vyjádřit strukturu systému a umožnit její simulaci. Převod CLD na tokový diagram musí vést k vytvoření alespoň jedné hladiny. Pokud se nám to nepodaří, snažíme se pravděpodobně modelovat statický systém. Každá hladina pak musí mít alespoň jeden přítok nebo odtok.
Základní premisou systémové dynamiky je, že k dynamickému chování dochází při akumulaci toků v hladinách. Lze tedy říci, že pokud nedochází k akumulaci toků v hladinách, nelze o dynamickém chování hovořit. Klíčovým prvkem každého dynamického modelu je tedy hladina (nazývaná také " stav" nebo "akumulace"). Jak bylo uvedeno v předchozím odstavci, účelem systémové dynamiky je matematicky vyjádřit strukturu systému a umožnit její simulaci. Převod CLD na tokový diagram musí vést k vytvoření alespoň jedné hladiny. Pokud se nám to nepodaří, snažíme se pravděpodobně modelovat statický systém. Každá hladina pak musí mít alespoň jeden přítok nebo odtok.
Z obrázku je patrné, že proměnná CDL je ve vývojovém diagramu reprezentována buď opět proměnnou, nebo hladinou. Šipka CLD se pak v diagramu toků stává buď tokem (přítokem nebo odtokem), nebo informačním spojem. Metoda převodu vývojových diagramů vyžaduje znalosti, které získáte v našich kurzech a literatuře. Postup tvorby manažerského simulátoru je popsán v úvodním obrázku tohoto článku. Stejně jako v případě CLD vytváříme počítačový model tak, aby dokázal odpovědět na otázku, podle které jsme vytvářeli příčinný smyčkový diagram. Projekt manažerského simulátoru lze popsat v pěti krocích:
1. Prvním krokem je vytvoření příčinného smyčkového diagramu pomocí nástrojů systémového myšlení.
2. Spuštění příslušného softwaru pro tvorbu systémově dynamických modelů.
3. Převod příčinného smyčkového diagramu na diagram toků pomocí příslušného specializovaného softwaru (nejlépe Vensim).
4. Hotový počítačový model nastavíme tak, aby simuloval scénáře s cílem najít odpověď na položenou otázku nebo otázky.
5. Odpovědi ověřené simulací použijeme k formulaci manažerských postupů, které povedou k dosažení požadovaných cílů.
1. Prvním krokem je vytvoření příčinného smyčkového diagramu pomocí nástrojů systémového myšlení.
2. Spuštění příslušného softwaru pro tvorbu systémově dynamických modelů.
3. Převod příčinného smyčkového diagramu na diagram toků pomocí příslušného specializovaného softwaru (nejlépe Vensim).
4. Hotový počítačový model nastavíme tak, aby simuloval scénáře s cílem najít odpověď na položenou otázku nebo otázky.
5. Odpovědi ověřené simulací použijeme k formulaci manažerských postupů, které povedou k dosažení požadovaných cílů.
Obrázek 2 ukazuje příklad vývojového diagramu (počítačového modelu) vytvořeného v simulačním software Vensim. Při vytváření simulačního modelu byla řešena otázka "Při jaké ceně bude zisk nejvyšší?". Možná vás napadne, že nejvyšší zisk bude při nejvyšší ceně. Pojďme společně prozkoumat platnost tohoto tvrzení. V následující tabulce najdete model vytvořený v tabulkovém procesoru, který říká, že při ceně 40 Kč za jednotku produktu u nás nakoupí 60. týden 21 472 zákazníků (1 zákazník - 1 nakoupený kus produktu) a dosáhneme kumulovaného (hrubého) zisku 70 230 421 Kč. Jen pro úplnost, zisk v 60. týdnu je v tabulkovém procesoru pochopitelně součinem počtu zákazníků a ceny produktu.
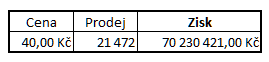
Na rozdíl od statických tabulkových modelů pokrývá dynamický simulační model všechny podstatné vlastnosti reálných systémů, a to:
a) zpětnou vazbu
b) zpoždění
c) nelineární vztahy mezi proměnnými
d) komplexitu
Proto lze očekávat, že výsledky simulace dynamického modelu se budou výrazně lišit od výsledků výpočtu tabulkového procesoru, přestože všechny vstupní parametry jsou v obou modelech stejné. Budeme simulovat stejné období - 60 týdnů s časovým krokem jeden týden.
a) zpětnou vazbu
b) zpoždění
c) nelineární vztahy mezi proměnnými
d) komplexitu
Proto lze očekávat, že výsledky simulace dynamického modelu se budou výrazně lišit od výsledků výpočtu tabulkového procesoru, přestože všechny vstupní parametry jsou v obou modelech stejné. Budeme simulovat stejné období - 60 týdnů s časovým krokem jeden týden.
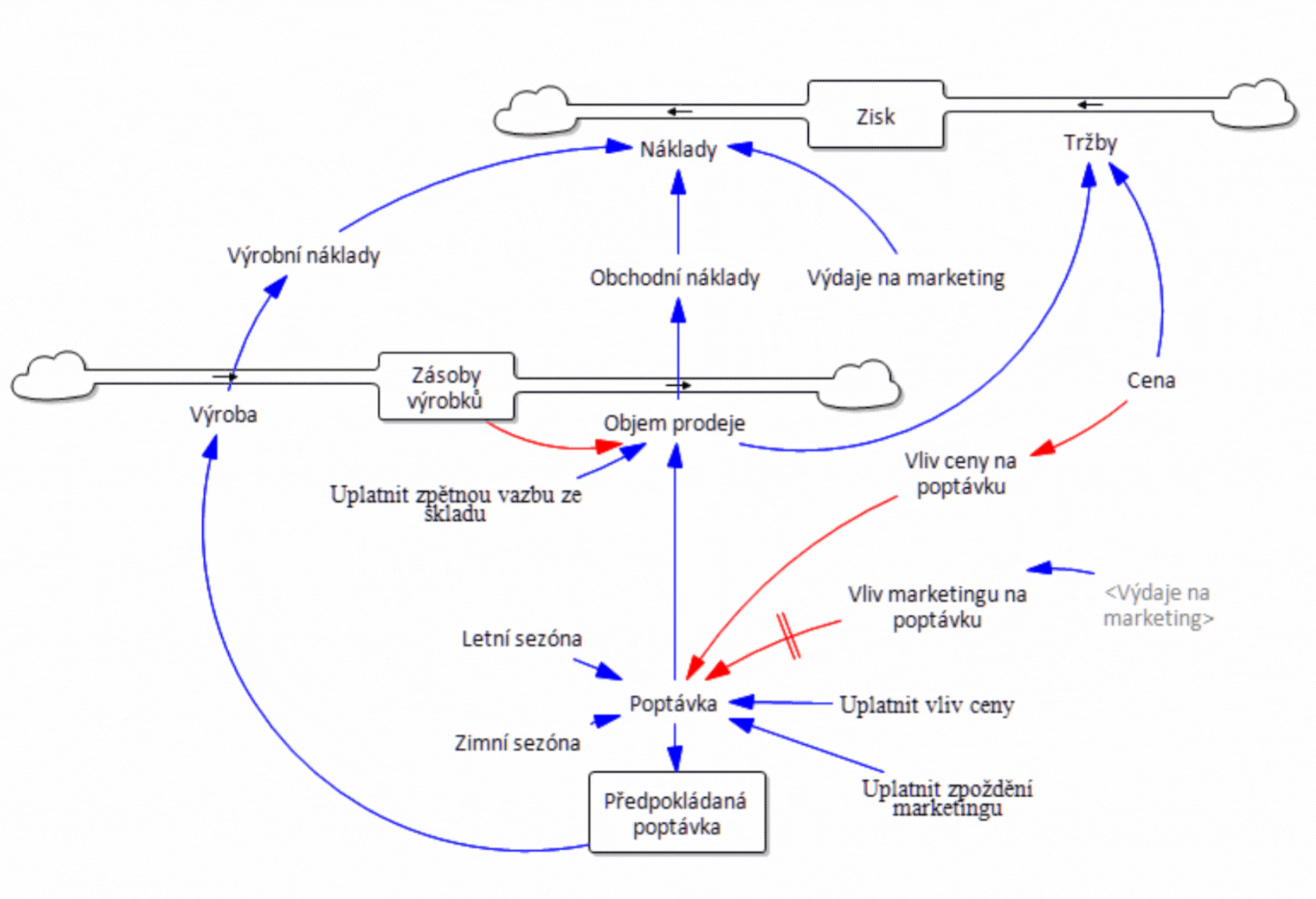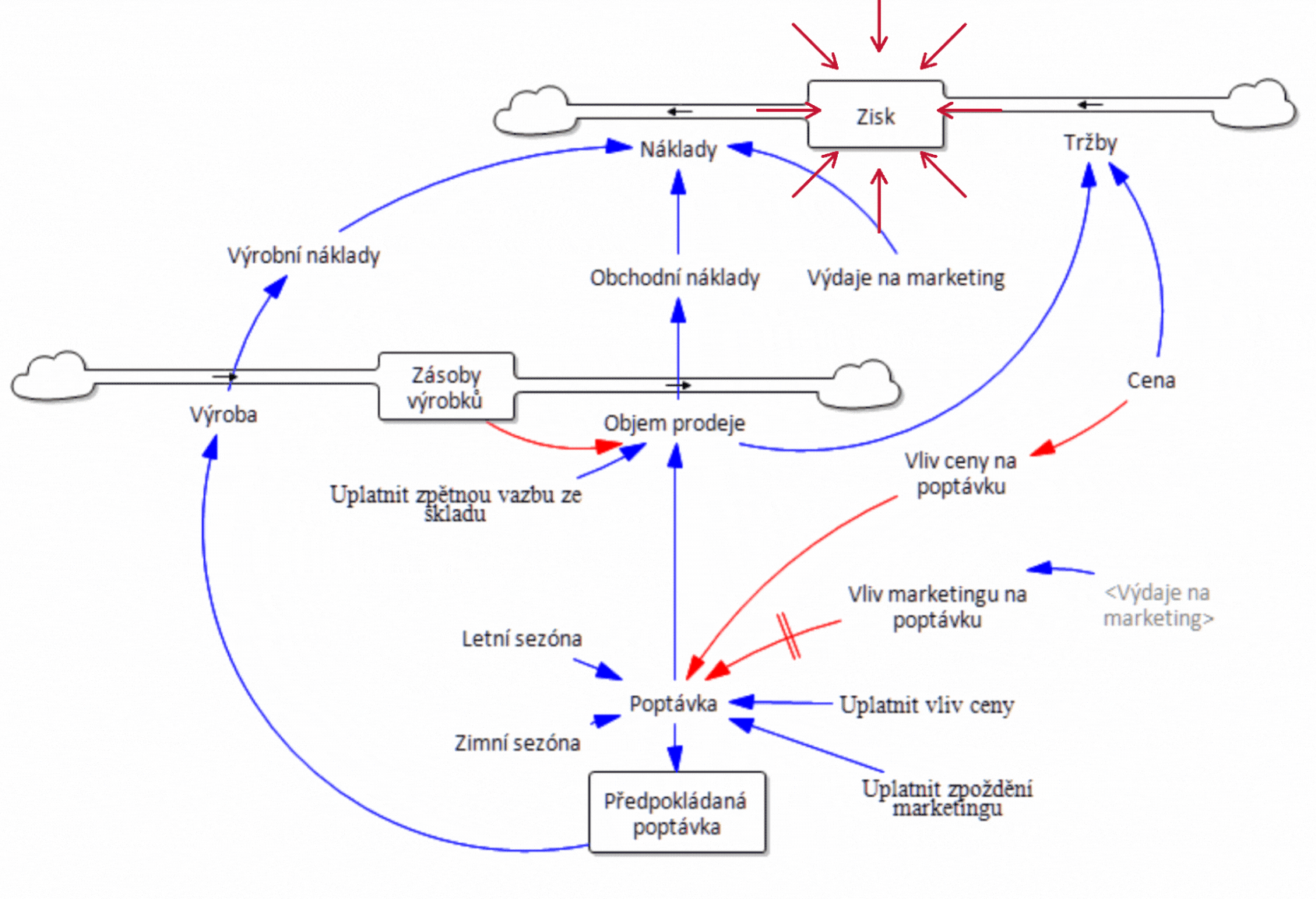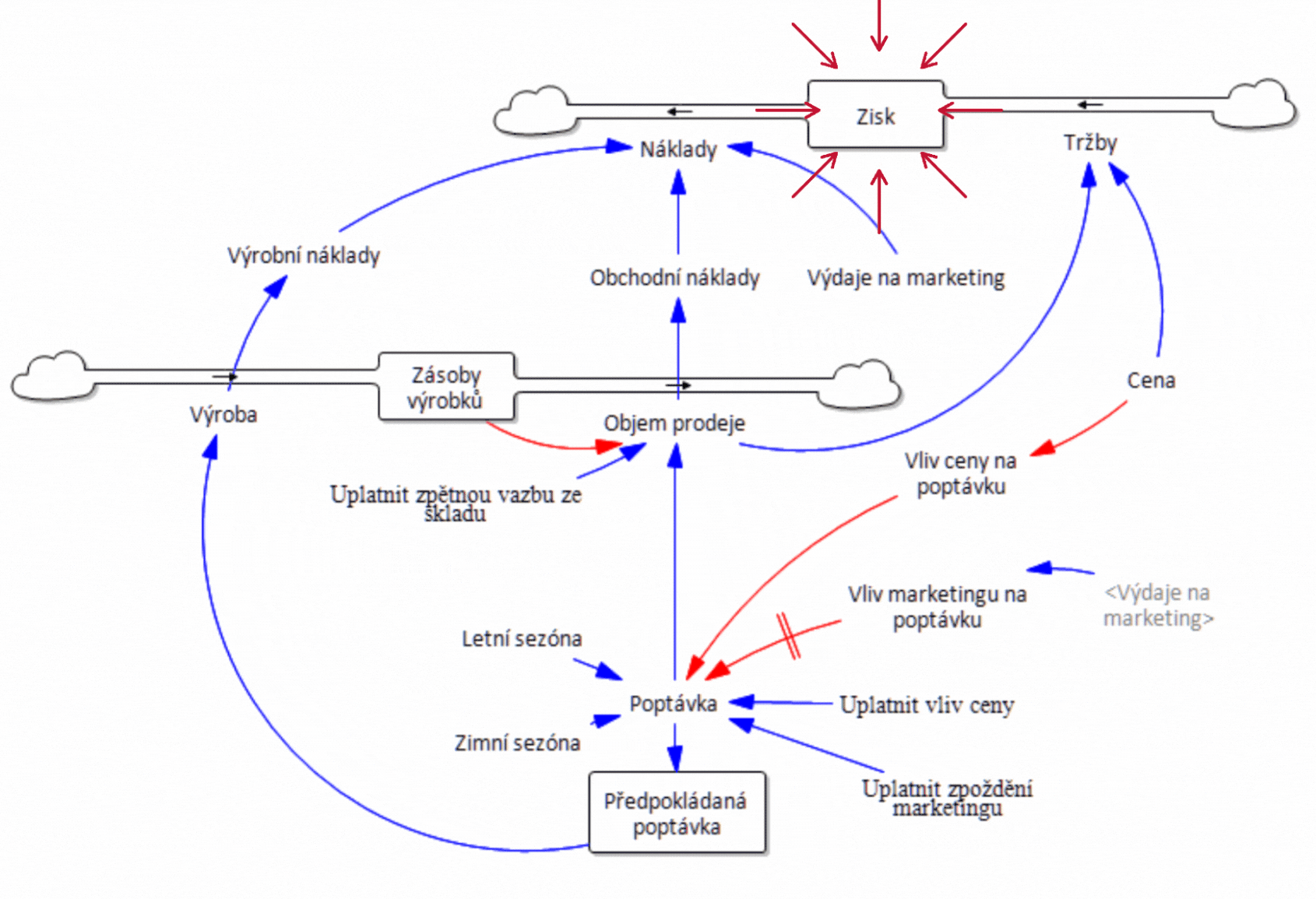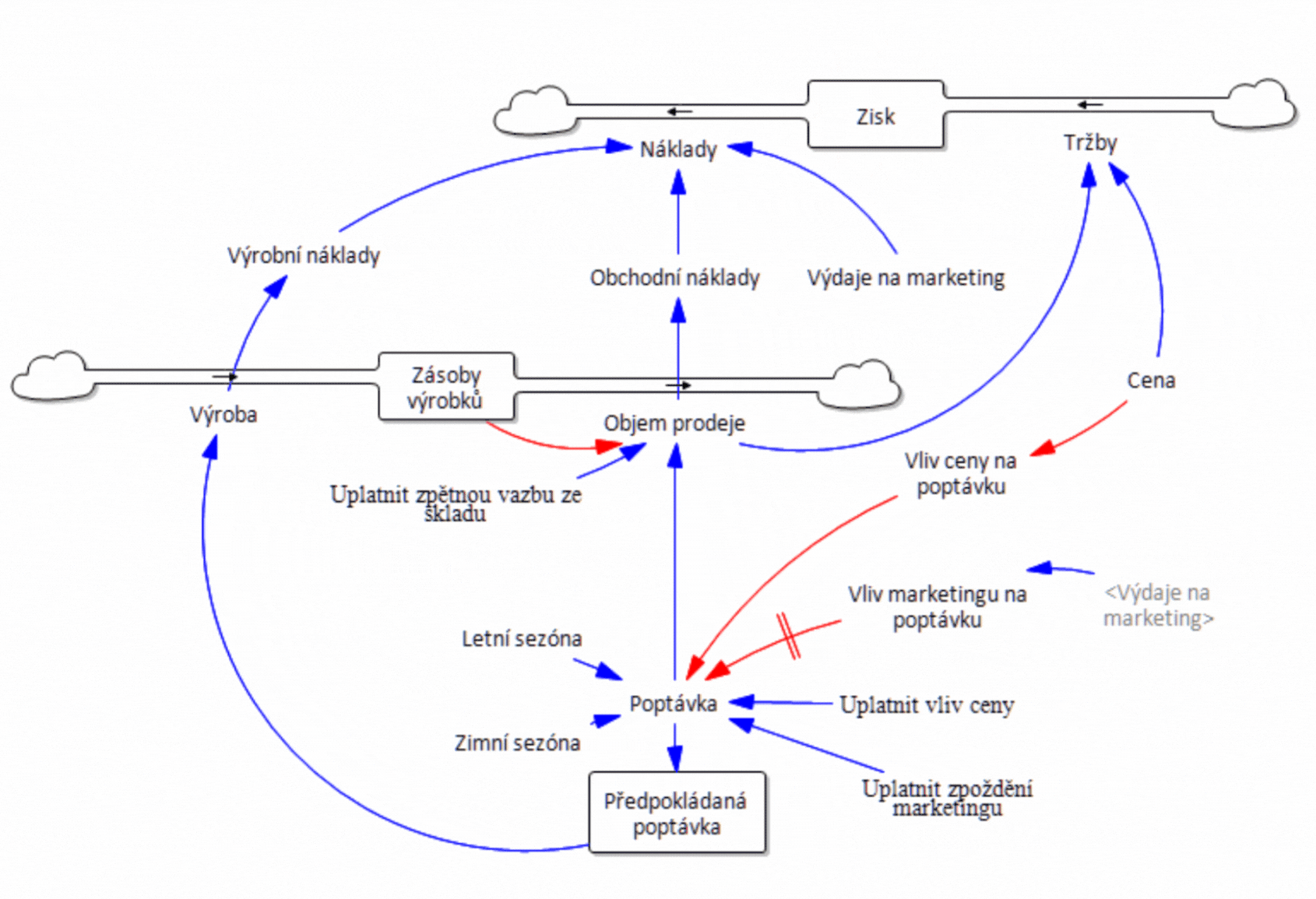
Obrázek 2 Diagram toků - simulační model - systémová struktura firmy vytvořená v simulačním softwaru.
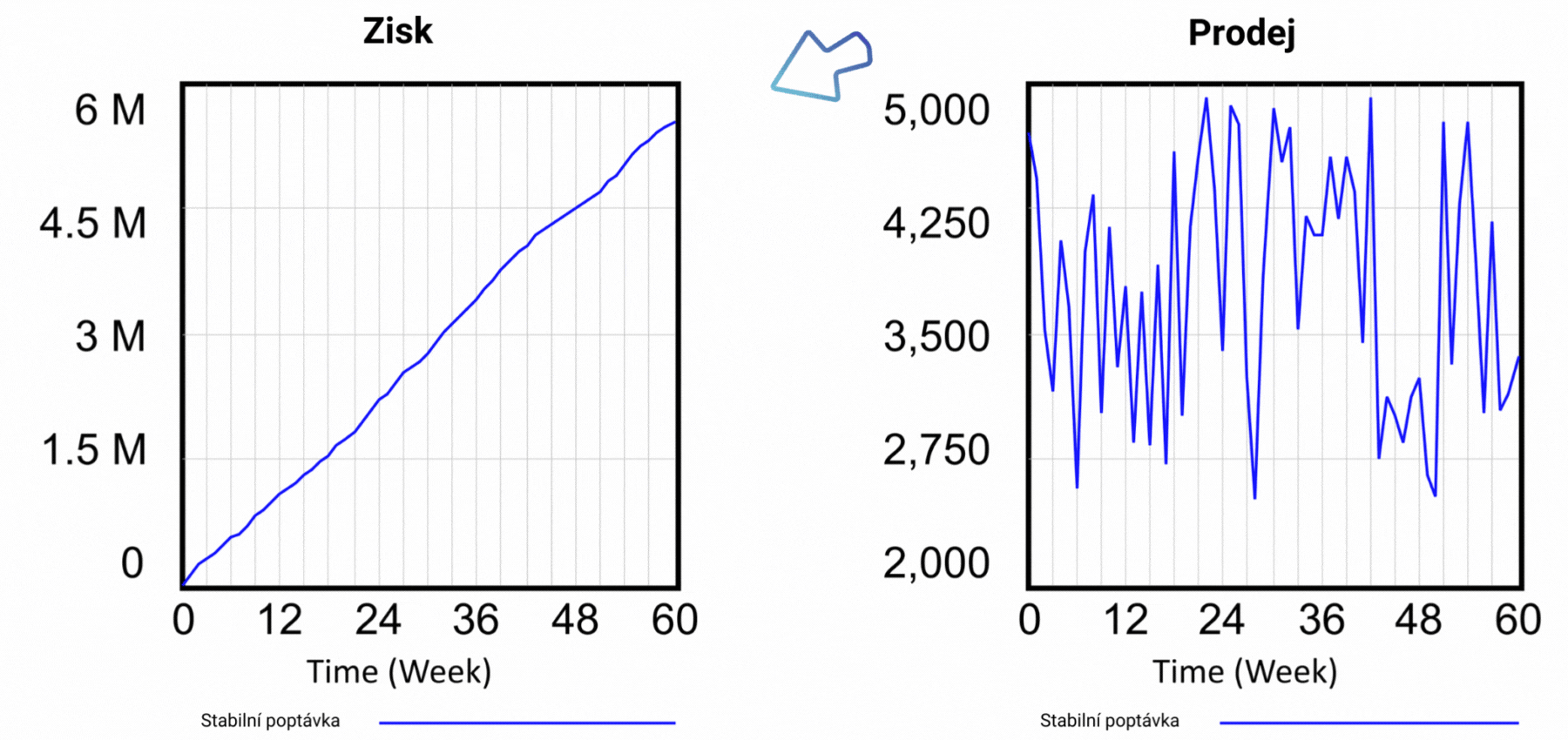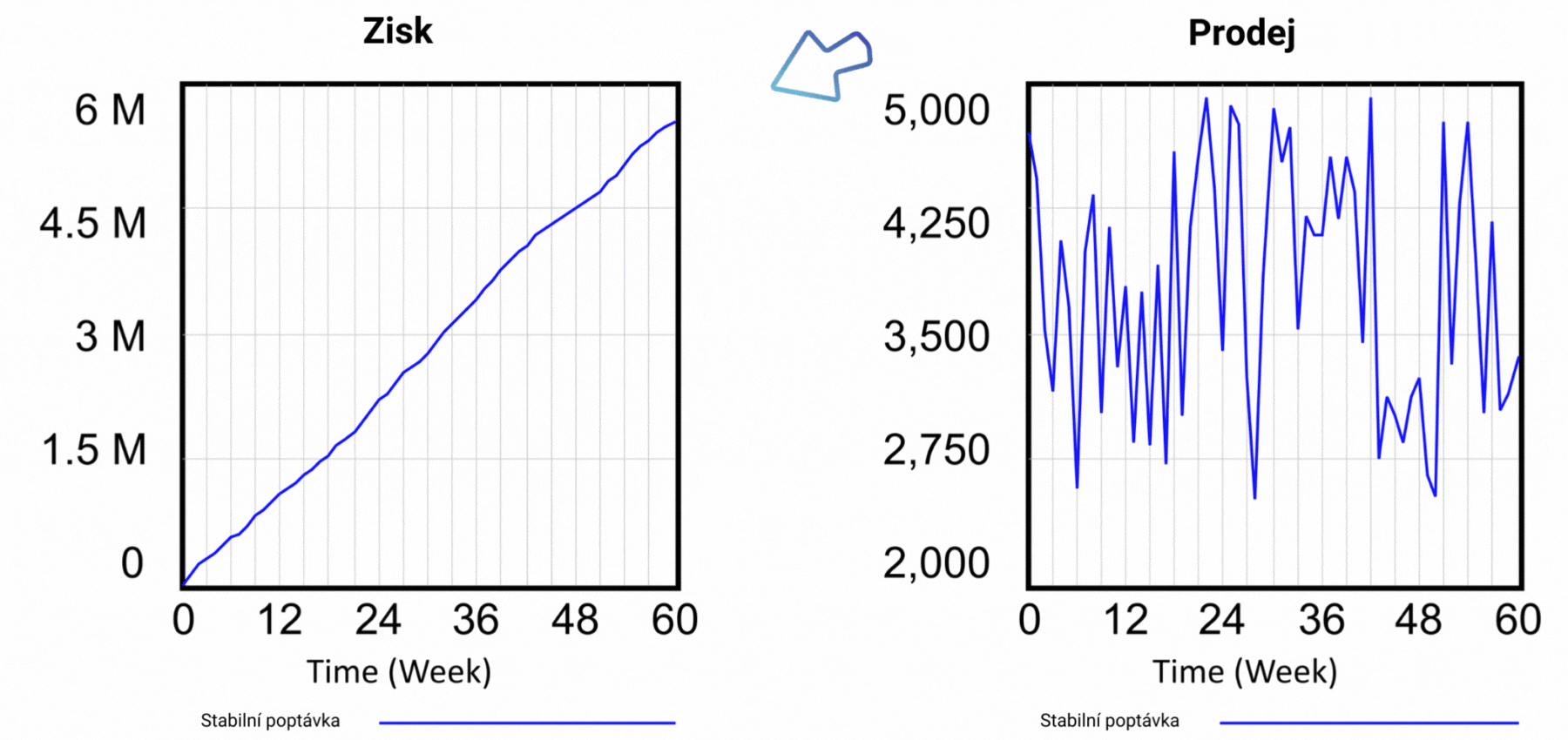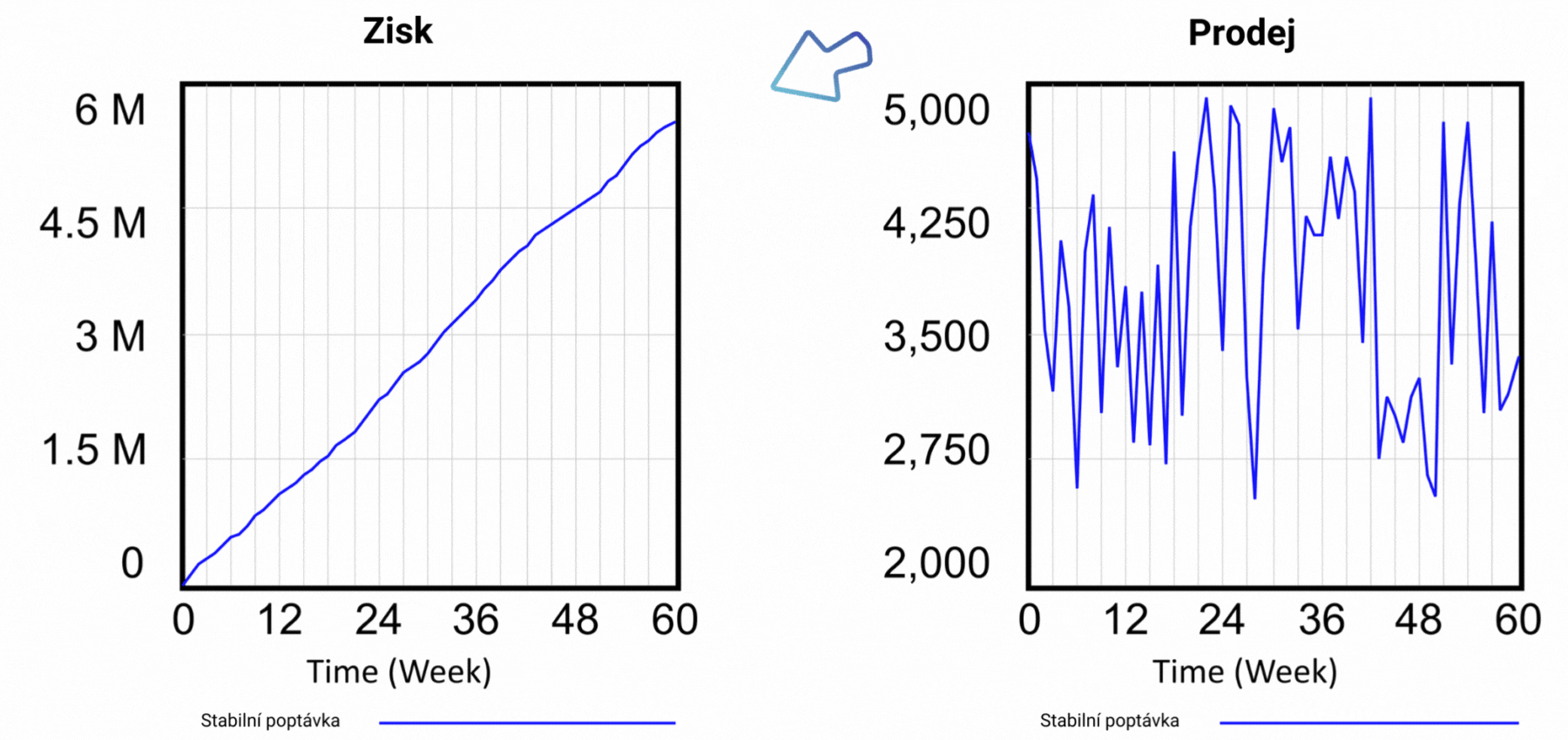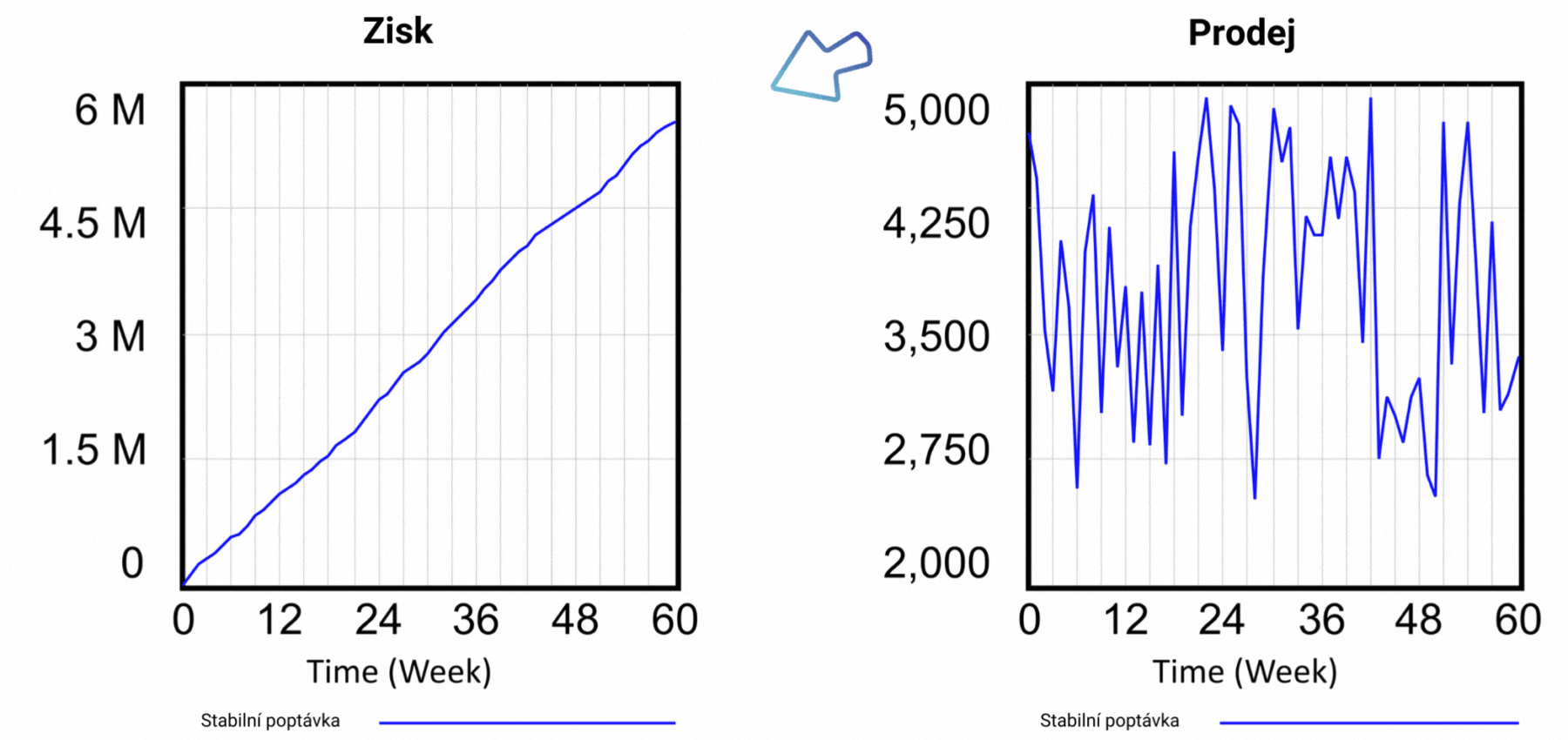
Obrázek 3 Výsledky simulace pro scénář s cenou 40 Kč za jednotku produktu.
Simulací scénáře, v němž jsme stanovili cenu za jednotku výrobku na 40 Kč, jsme zjistili, že počet zákazníků na konci období i dosažený zisk jsou výrazně nižší, než jak ukazuje statický tabulkový model. Výsledky simulace jsou vidět na obrázku 3. Po šedesáti týdnech jsou prodeje na úrovni 3 355 jednotek výrobku a dosažený zisk činí 5 547 000 Kč. Předpokládejte, že jeden z modelů je blíže skutečnosti, který z nich to je? Statický model v tabulkovém procesoru, nebo dynamický model ve Vensimu? Podívejte se na strukturu vývojového diagramu na obrázku 2, konkrétně na vliv proměnné Cena na chování modelu. Zjistíme, že Cena se používá k výpočtu Tržeb. Výpočet Tržeb je v obou modelech triviální: Tržby = Cena * Prodeje. Jinými slovy, cena za jednotku se vynásobí počtem prodaných jednotek. Dynamický model oproti statickému obsahuje Vliv ceny na poptávku. Vyjadřuje tak obecnou zkušenost, že příliš vysoká cena povede k menšímu zájmu o výrobek, a jakmile je překročena určitá hranice, nikdo už nebude mít o produkt zájem.
Má smysl zavádět taková pravidla do modelu? Pokud chceme skutečně vědět, jak se bude náš podnik chovat, není pochyb o tom, že to smysl má. K čemu je model, který nám říká, že budeme mít zisk 70 milionů, když ve skutečnosti bude desetkrát nižší? Proč tedy do našeho statického tabulkového modelu nevložíme vztah mezi cenou výrobku a poptávkou? Protože tento vztah je nelineární a ve statických modelech musíme v samostatné tabulce vytvořit nelineární funkci, která ovlivní výslednou hodnotu poptávky. Složitost řešení je jedním z důvodů, proč se ve statických modelech nelineární vztahy mezi proměnnými zanedbávají a výsledky pak postrádají smysl. V dynamickém modelu k tomu stačí jediná proměnná, v níž se pomocí myši nastaví průběh předpokládaného vztahu mezi cenou a jejím vlivem na poptávku (Vliv ceny na poptávku), jak je znázorněno na obrázku 4. Během několika sekund je možné nastavit libovolný vztah mezi proměnnými a modelovat měkké proměnné, které se ve statických modelech nevyskytují, přestože ve skutečnosti mají na výsledné chování klíčový vliv.
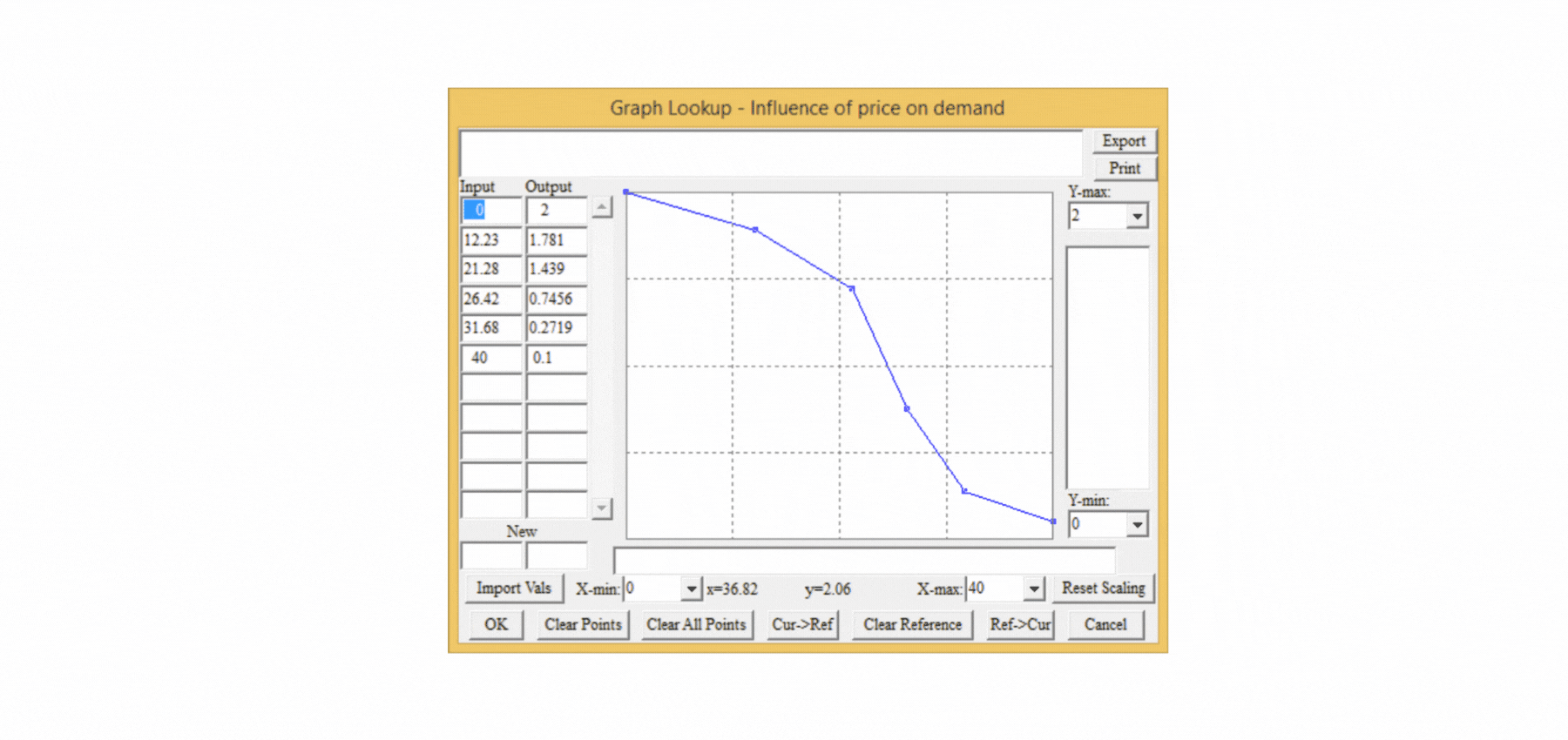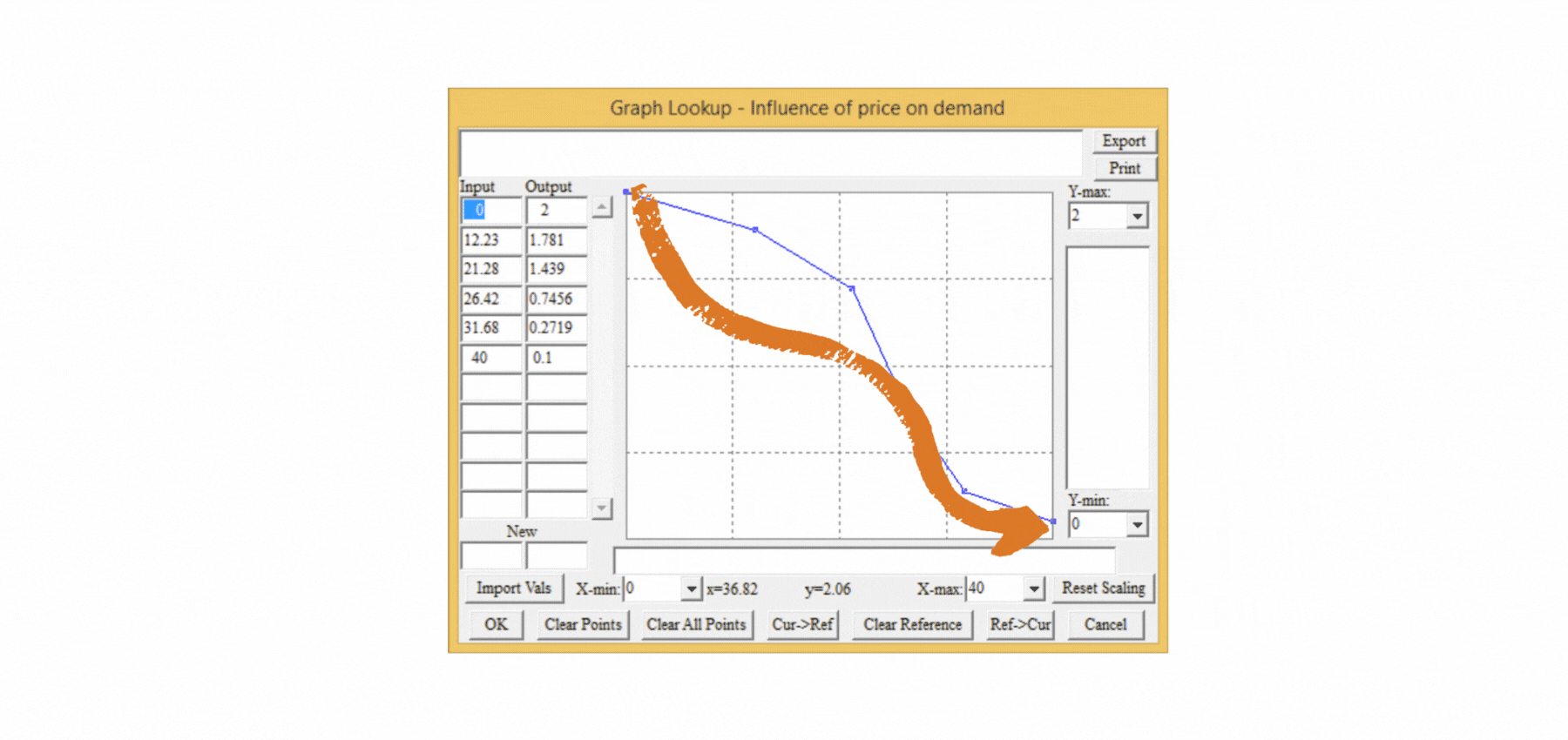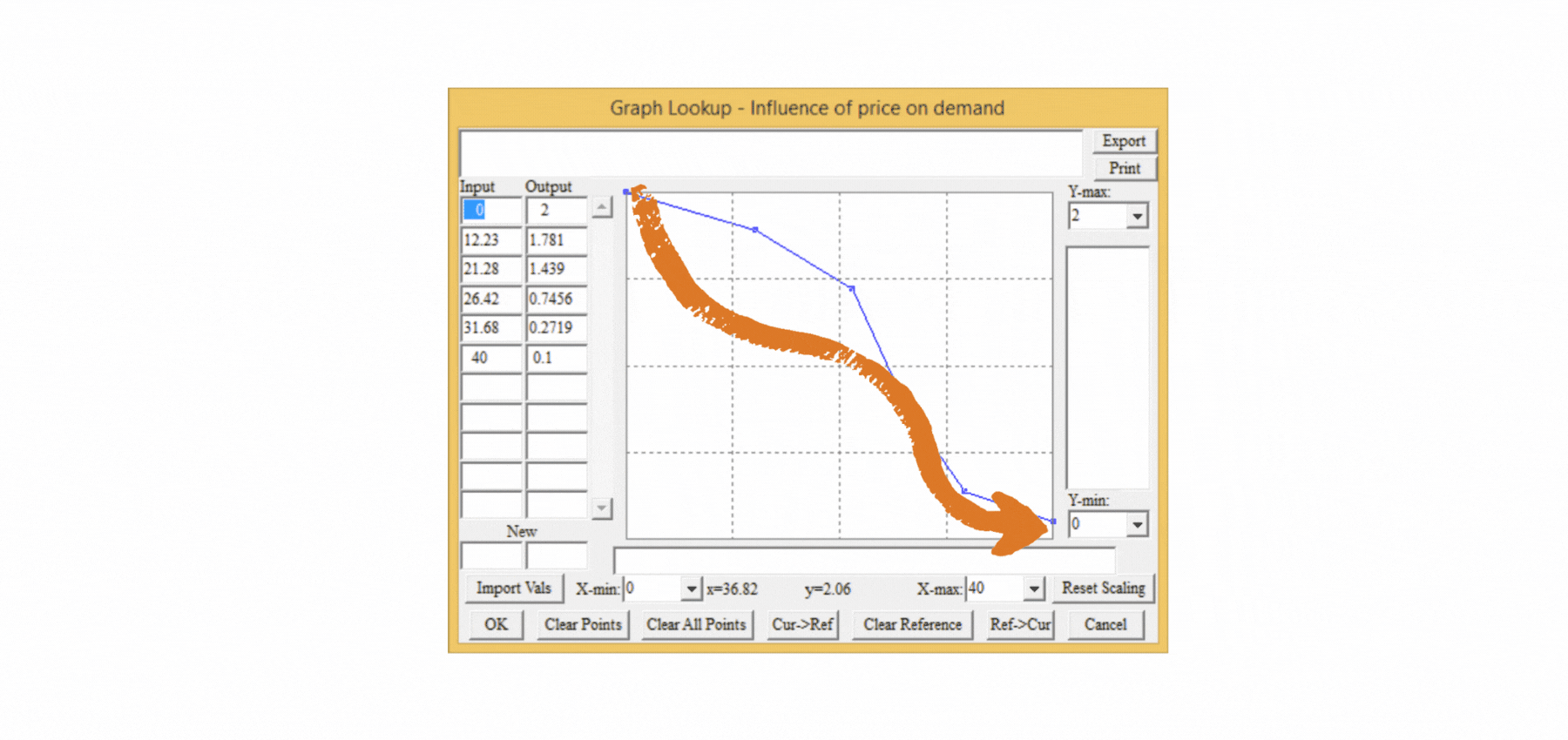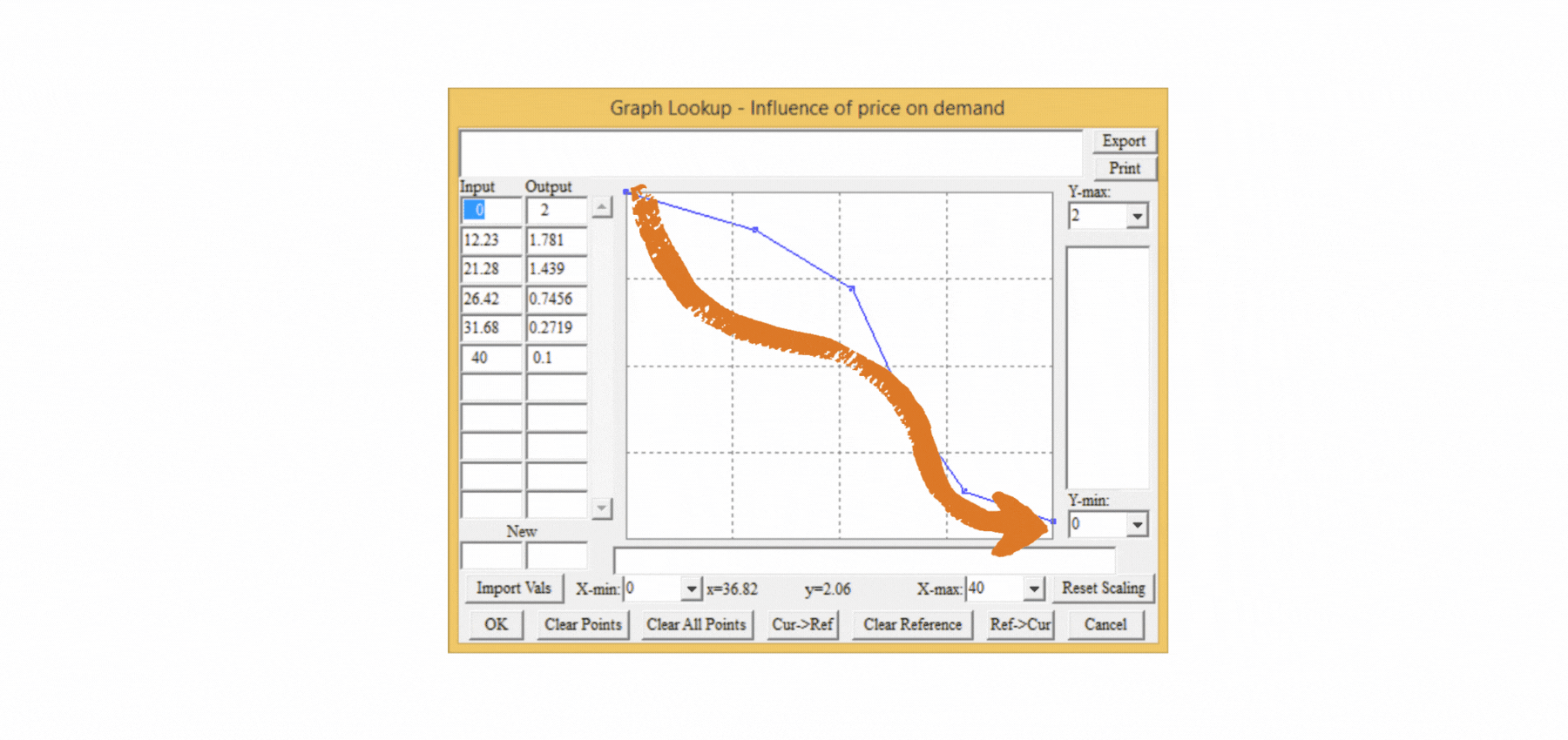
Obrázek 4 Snadný způsob nastavení nelineárního vztahu mezi proměnnými v dynamickém modelu.
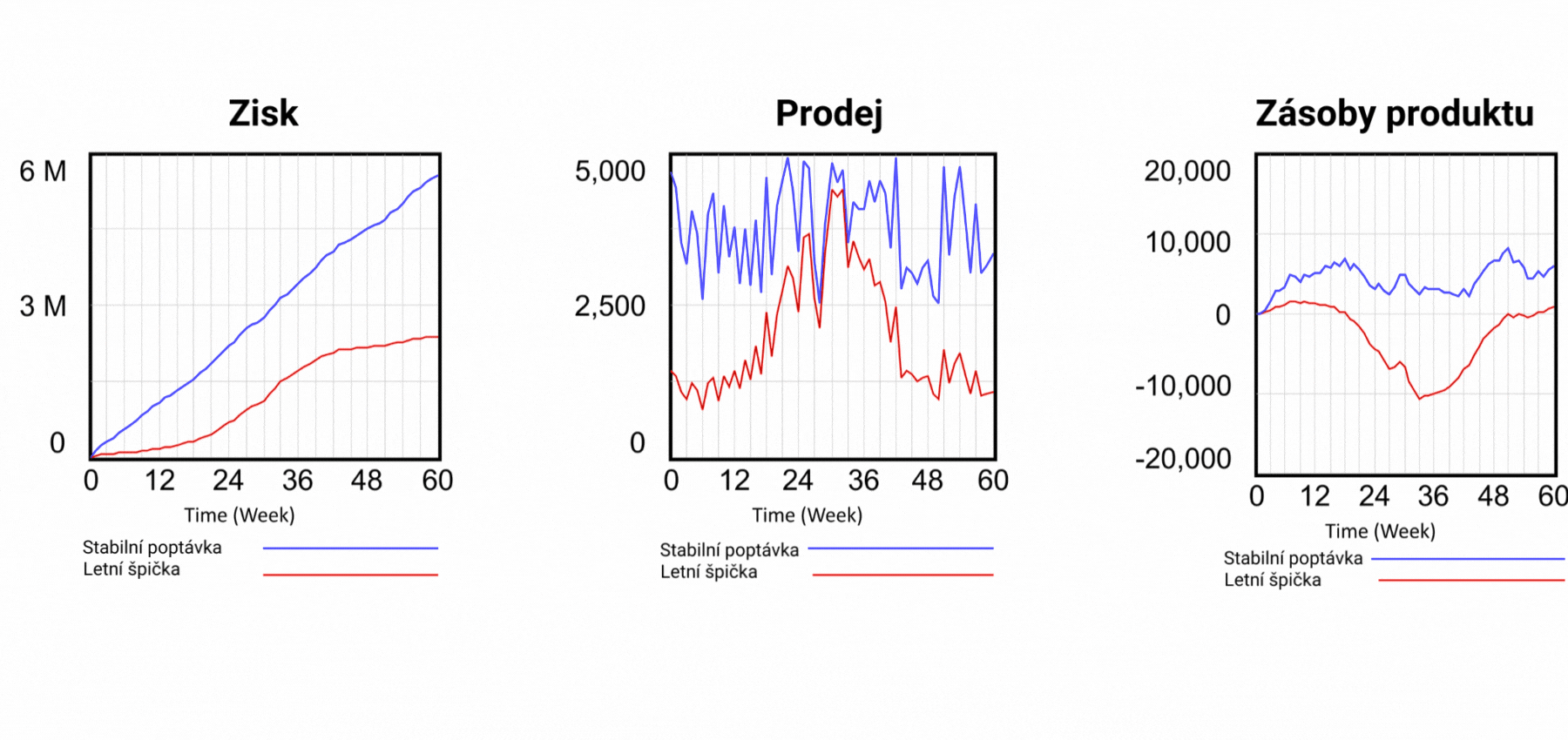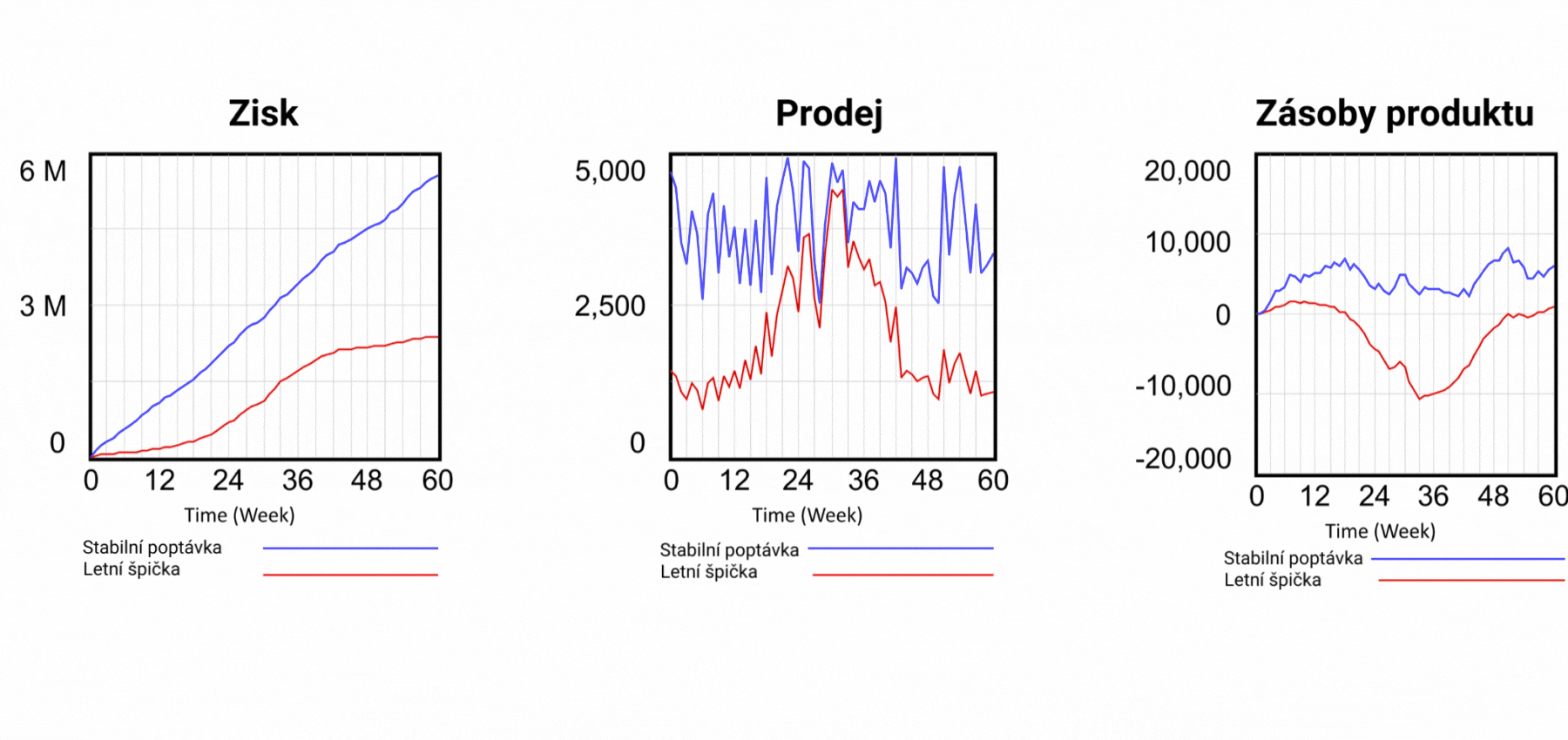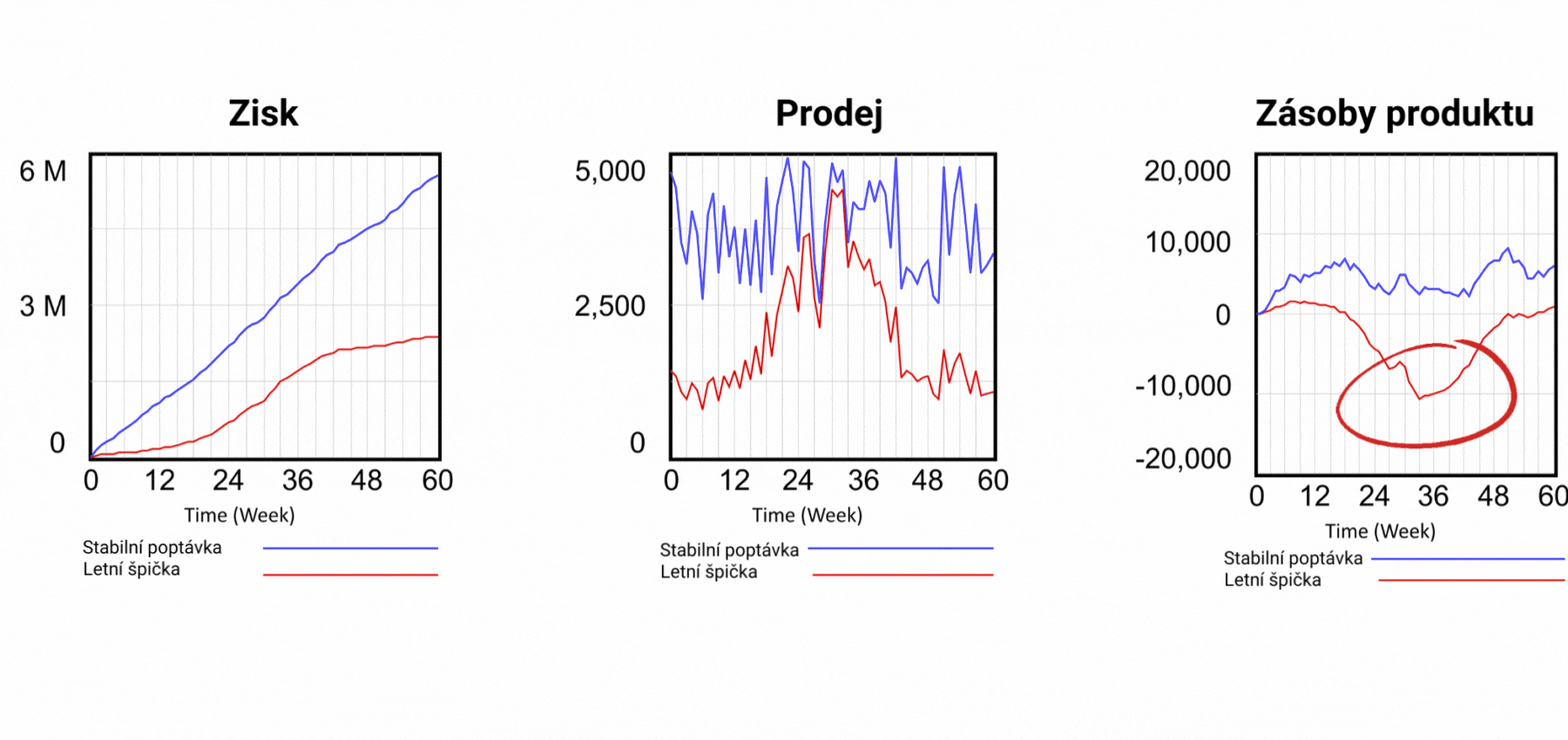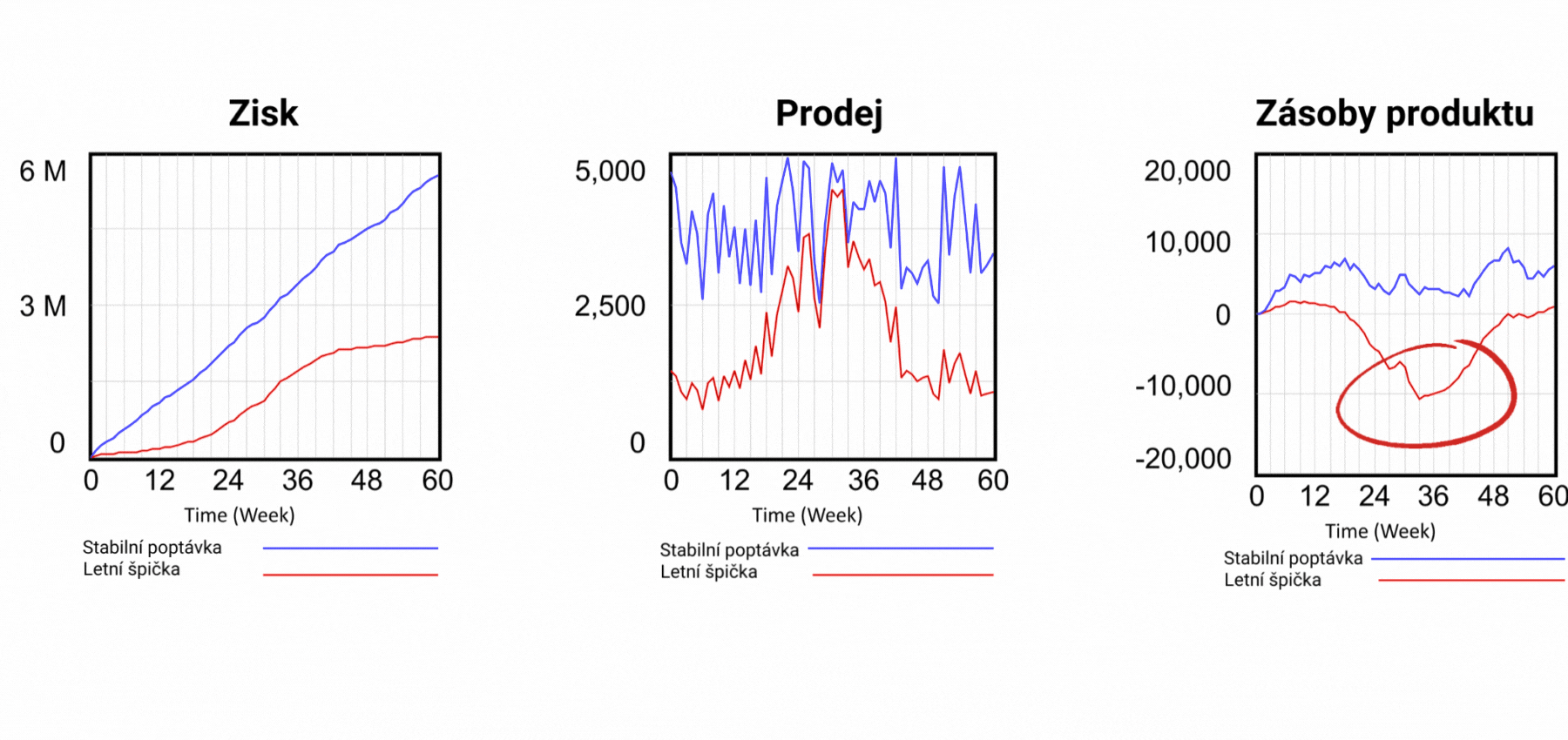
Obrázek 5 Výsledky simulačních scénářů a detail zásob produktu.
Tím však problémy s tabulkovými procesory nekončí. Podívejme se nyní na výrobní část našeho modelu. V tabulkovém procesoru není nic k vidění. Netušíme, jak jsou prvky modelu propojeny, musíme zkoumat každou buňku zvlášť, abychom zjistili, co ovlivňuje její hodnotu. V diagramu toků je logika modelu vyjádřena graficky. Okamžitě vidíme, že aktuální poptávka slouží k výpočtu předpokládané poptávky a předpokládaná poptávka určuje výrobu. Výroba vyrábí produkty, které jdou do skladu produktů a odtud jsou expedovány k zákazníkovi. Nastavme nyní náš dynamický model opět přesně podle statického modelu a podívejme se na průběh prodeje. Model pracuje se dvěma režimy poptávky. Letním a celoročním, tzv. stabilním. Zatím jsme pracovali s tím stabilním. Celkový součet poptávaných produktů je pro oba režimy stejný, liší se pouze rozložení poptávky v simulovaném období. Letní průběh je charakterizován nízkou poptávkou v zimě a vysokou poptávkou v létě. Letní průběh poptávky je vyjádřen na obrázku 4 červenou křivkou Prodej.
Z hlediska zisku je letní scénář méně úspěšný, ale podívejte se na poslední graf, který ukazuje zásoby produktu. Červený průběh dokládá, že zásoby letního scénáře jsou v záporných hodnotách! Znamená to tedy, že prodáváme produkt, který nemáme. Jak je to možné? Při pohledu na strukturu na obrázku 2 vidíme, že hodnota Prodeje určuje odtok ze skladových zásob produktu. Prodej je řízen pouze poptávkou, nic jiného mu nebrání a hodnota Zásoby nemá na Prodej žádný vliv. V realitě to však takto nefunguje. Pokud prodáváme produkt, musíme jej zákazníkovi skutečně dodat, jinak se vystavujeme riziku postihu za podvod. Existuje nějaké řešení problému prodeje neexistujících produktů? V dynamickém modelu je velmi snadné. Jednoduše přidáme zpětnou vazbu ze zásoby výrobků k definici Prodeje a řekneme, že Prodej nemůže být vyšší než Zásoba hotových výrobků, jak je uvedeno na obrázku 6. Ve výstupních grafech vidíme, že ani v letním scénáři neklesne zásoba pod nulu, a zpětná vazba tedy funguje! Na obrázku 2 je zpětná vazba od zásoby výrobků k prodeji zvýrazněna červenou barvou. Lze tento problém řešit i v tabulkovém procesoru? Odpověď vás možná překvapí - nelze. Tabulkový procesor při pokusu o vytvoření zpětné vazby zobrazí chybové hlášení, že se pokoušíte vytvořit nedovolenou cirkulární závislost. Problém je v tom, že podstata všech systémů na tomto světě je založena na cirkulárních závislostech! To tedy znamená, že modely reálného světa nelze v tabulkovém procesoru vytvořit.
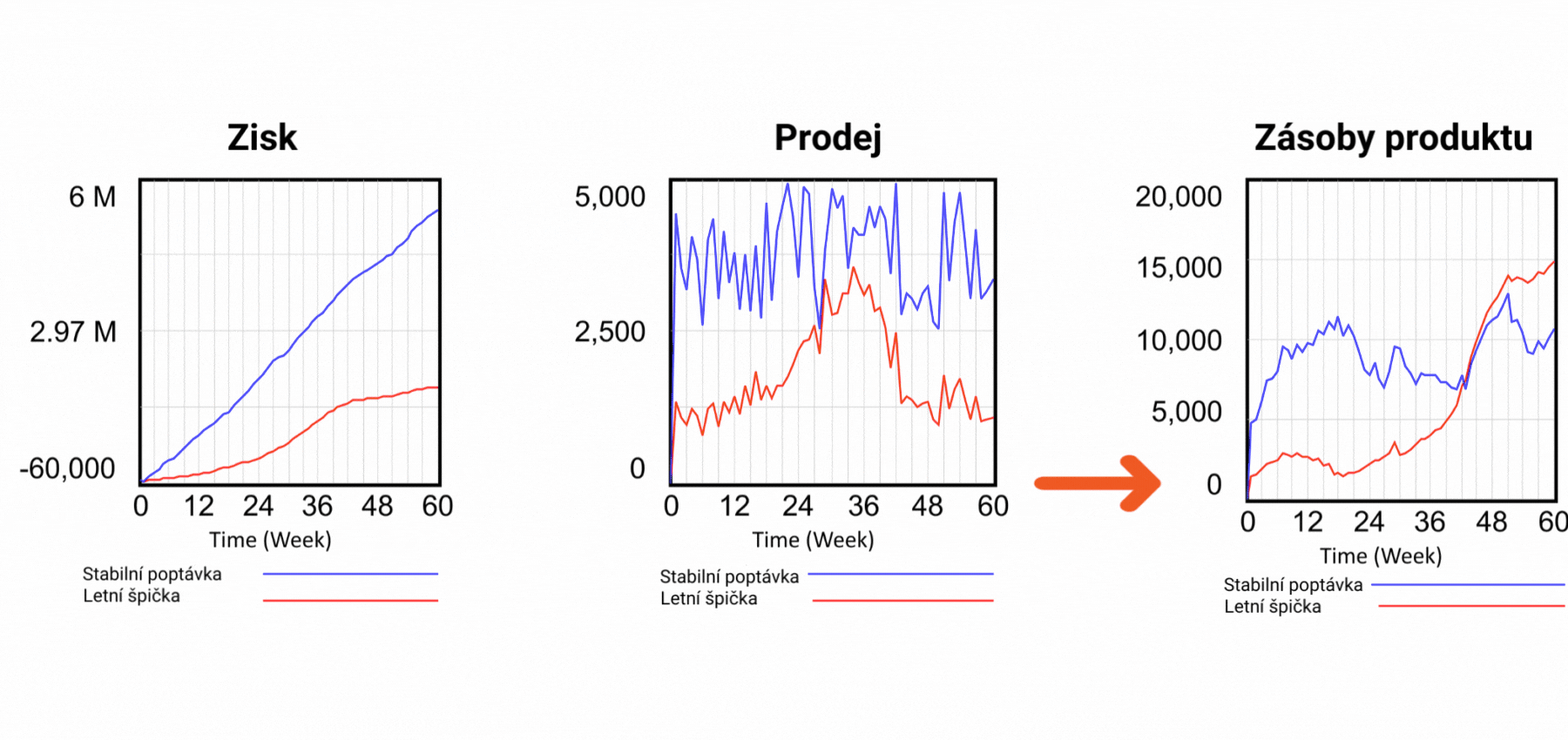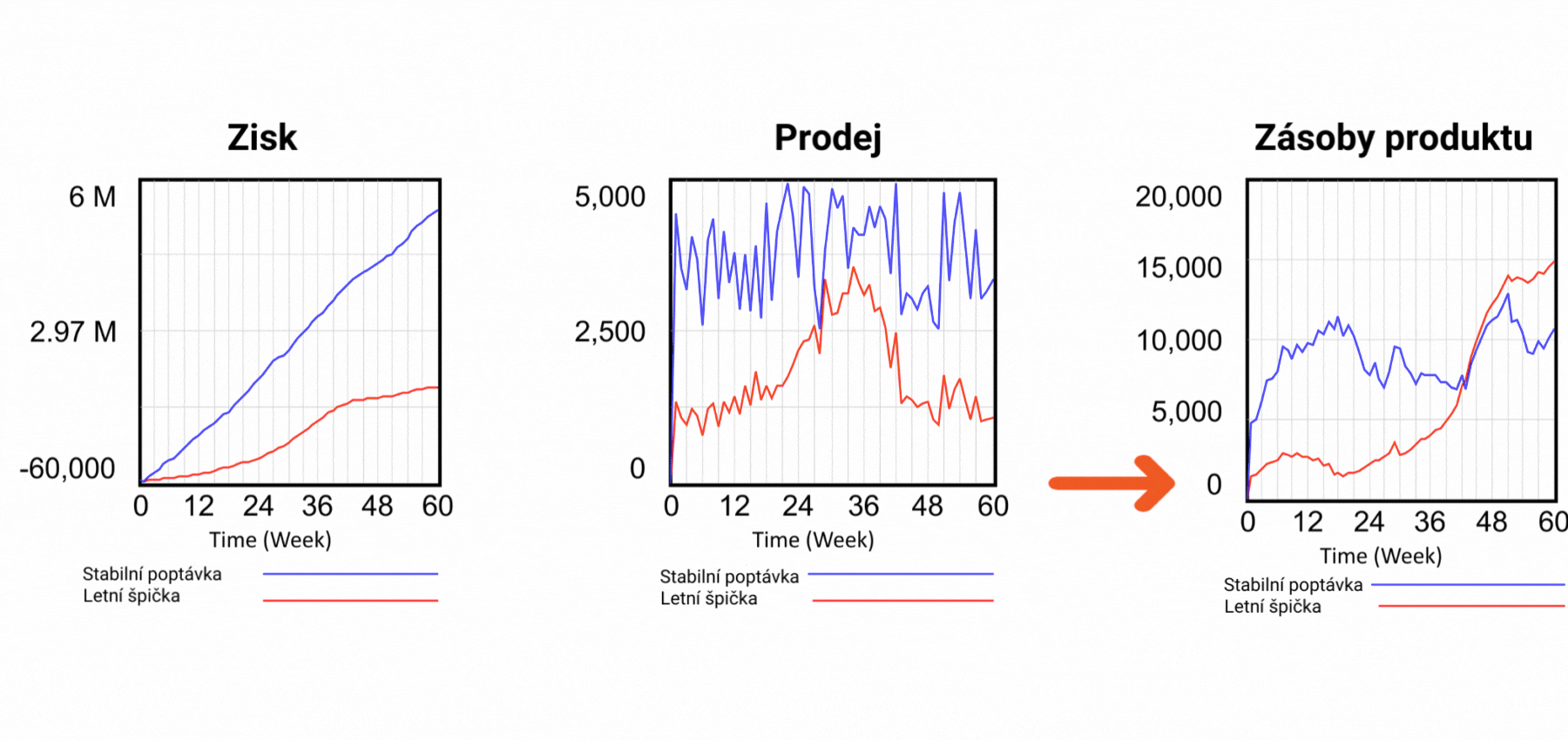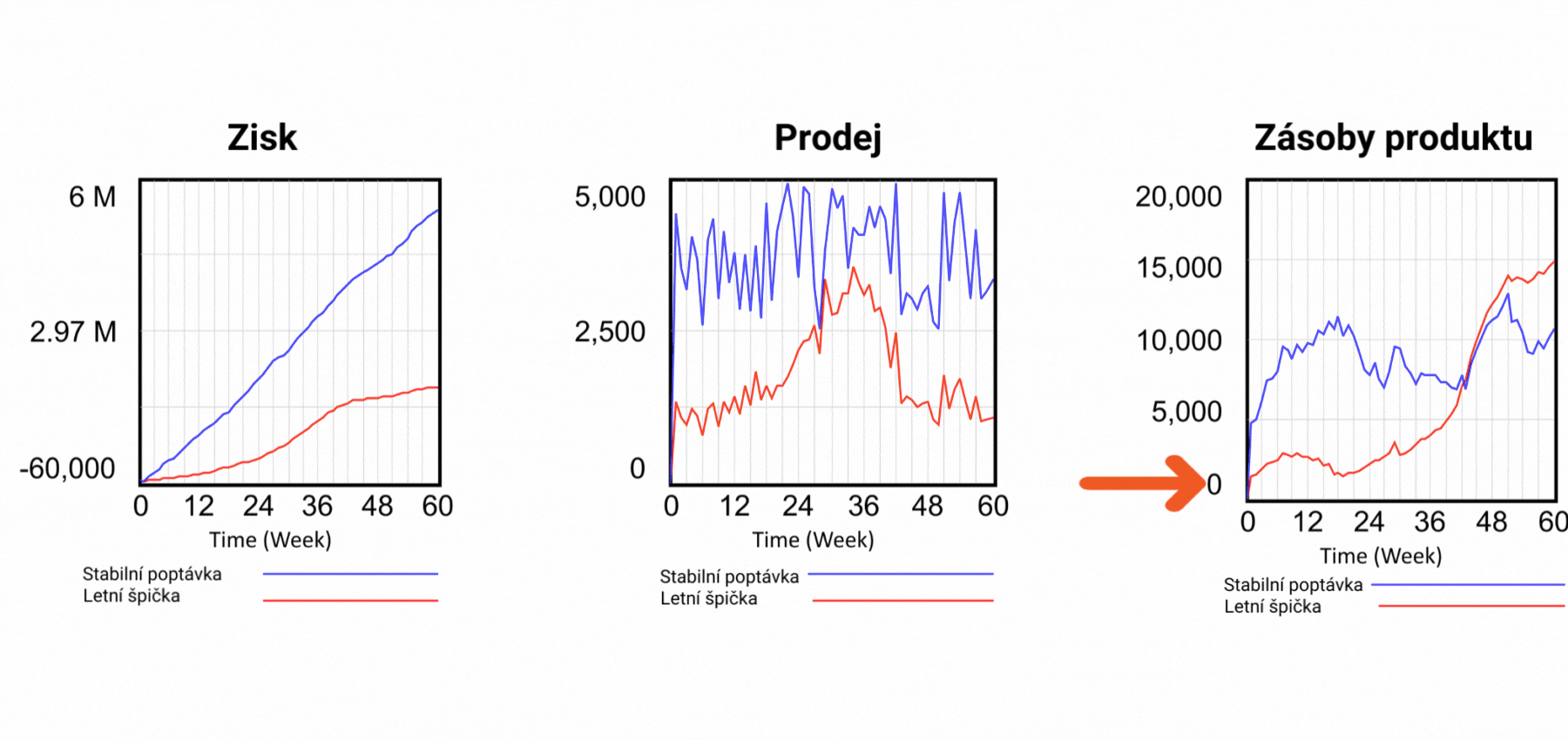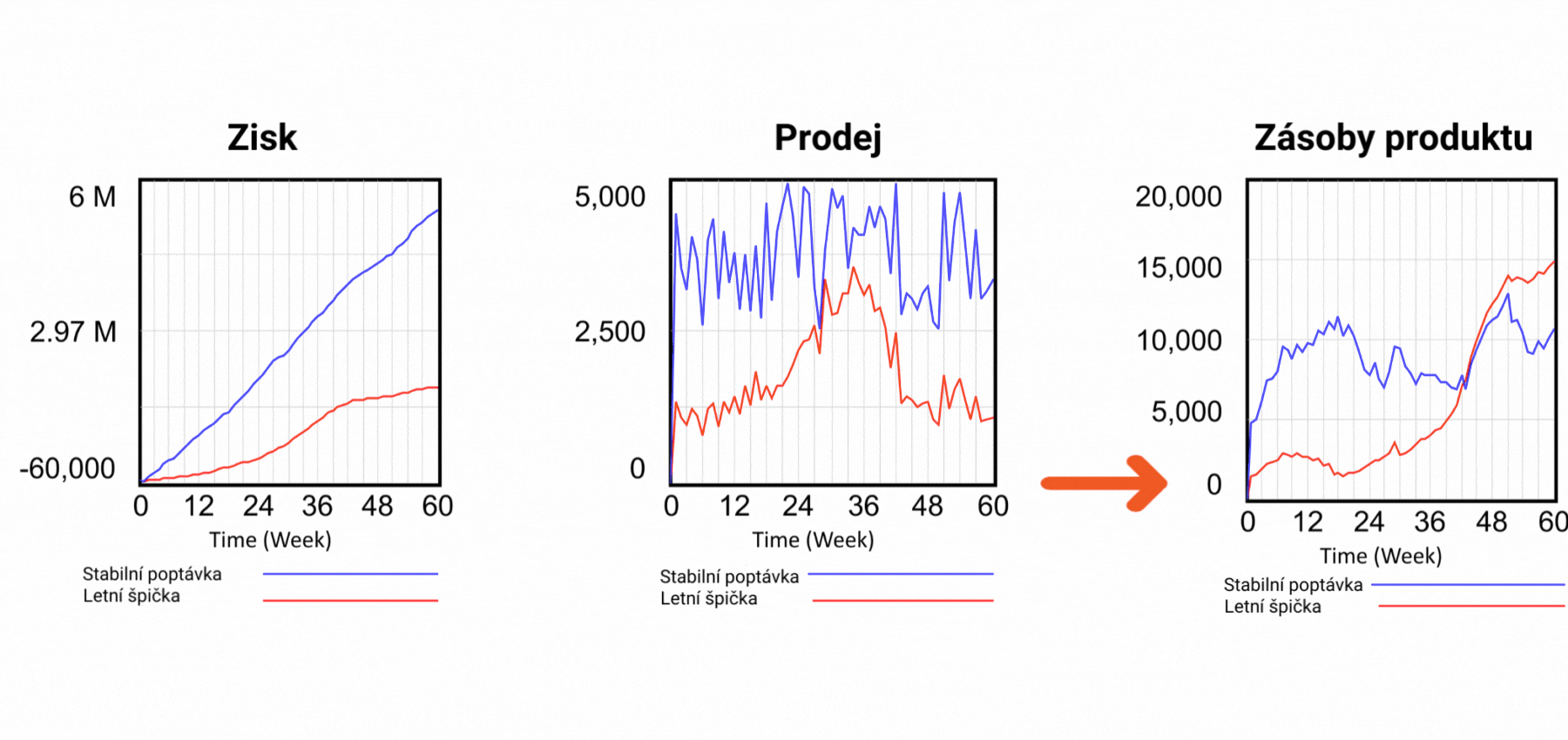
Obrázek 6 Simulace scénářů se zpětnou vazbou, která zabraňuje prodeji neexistujících produktů.
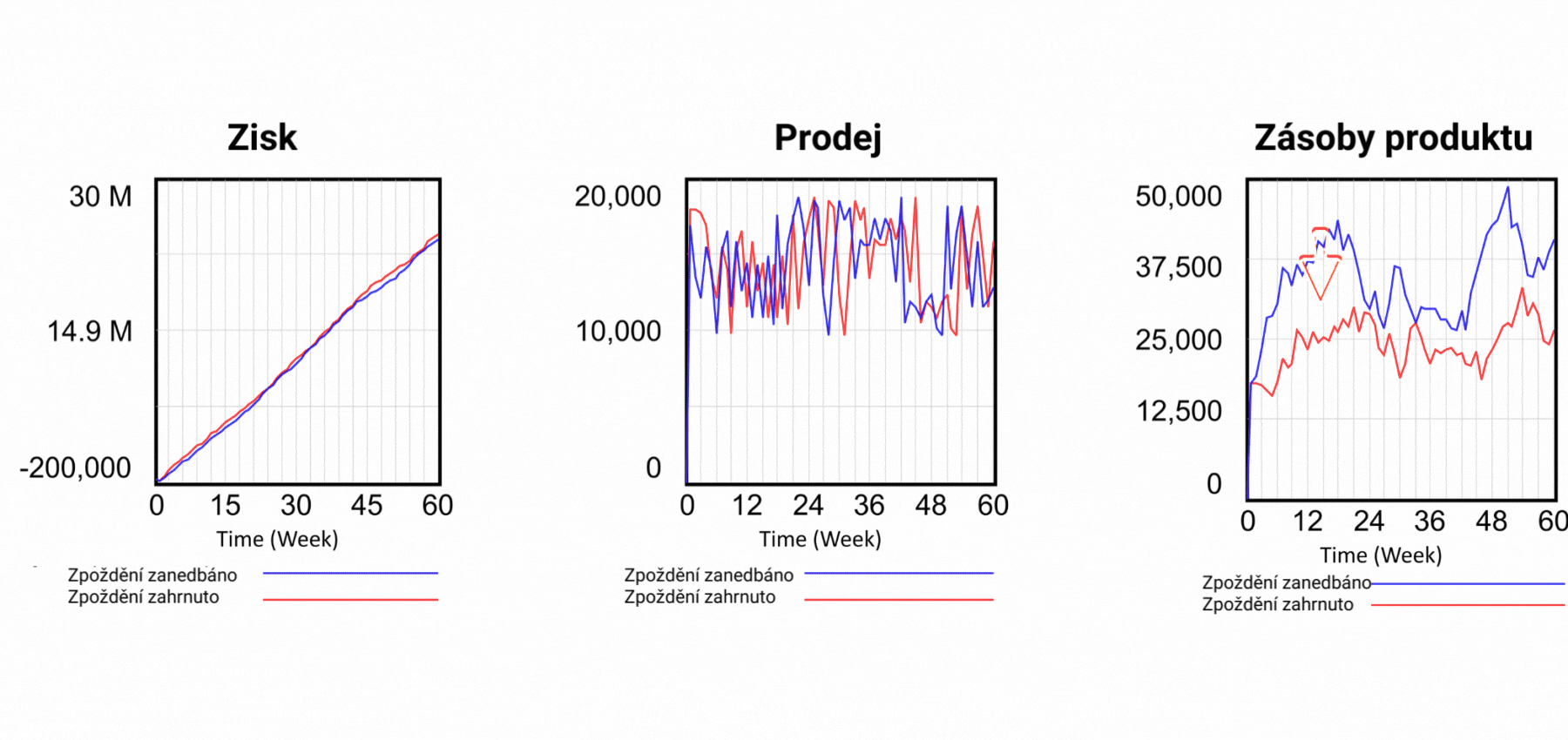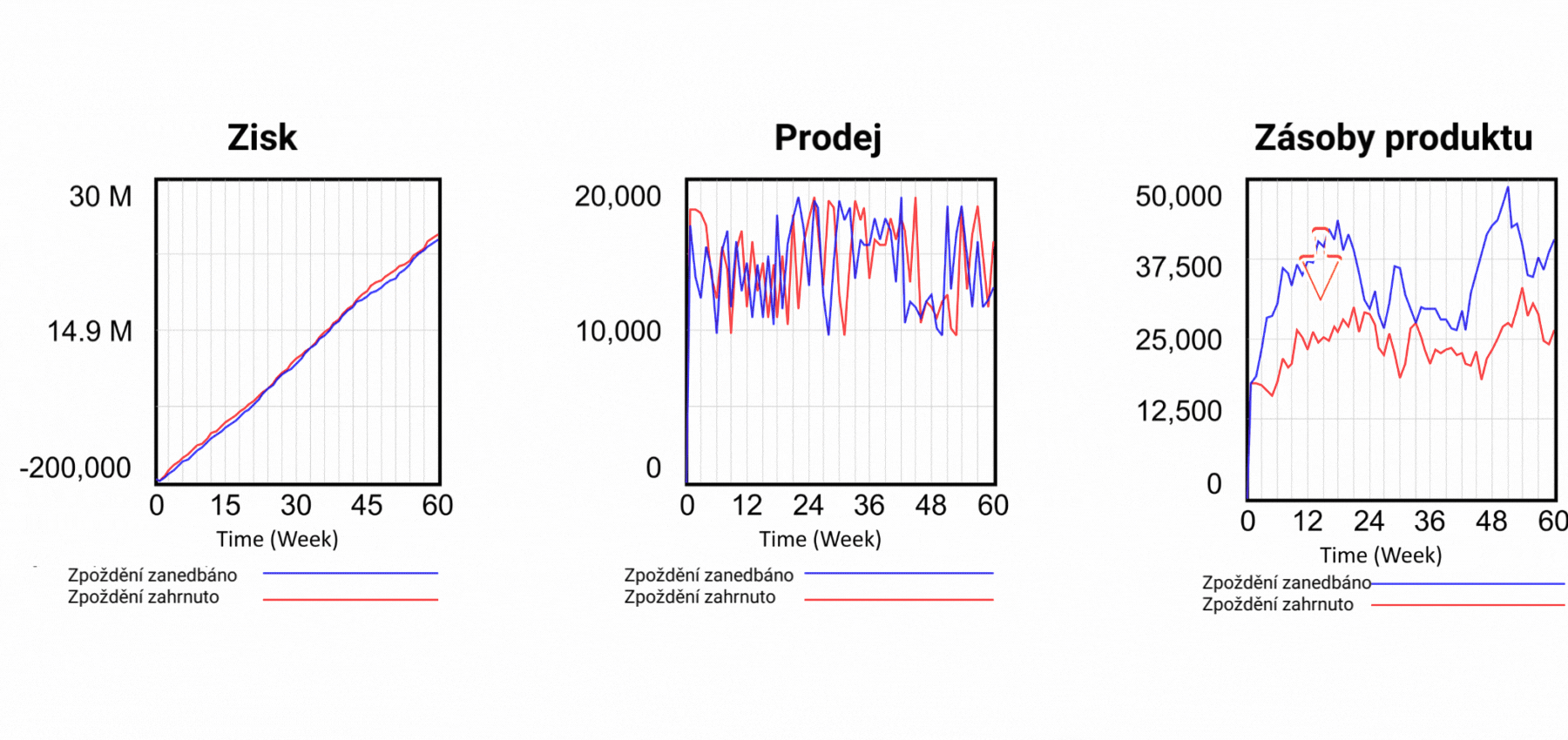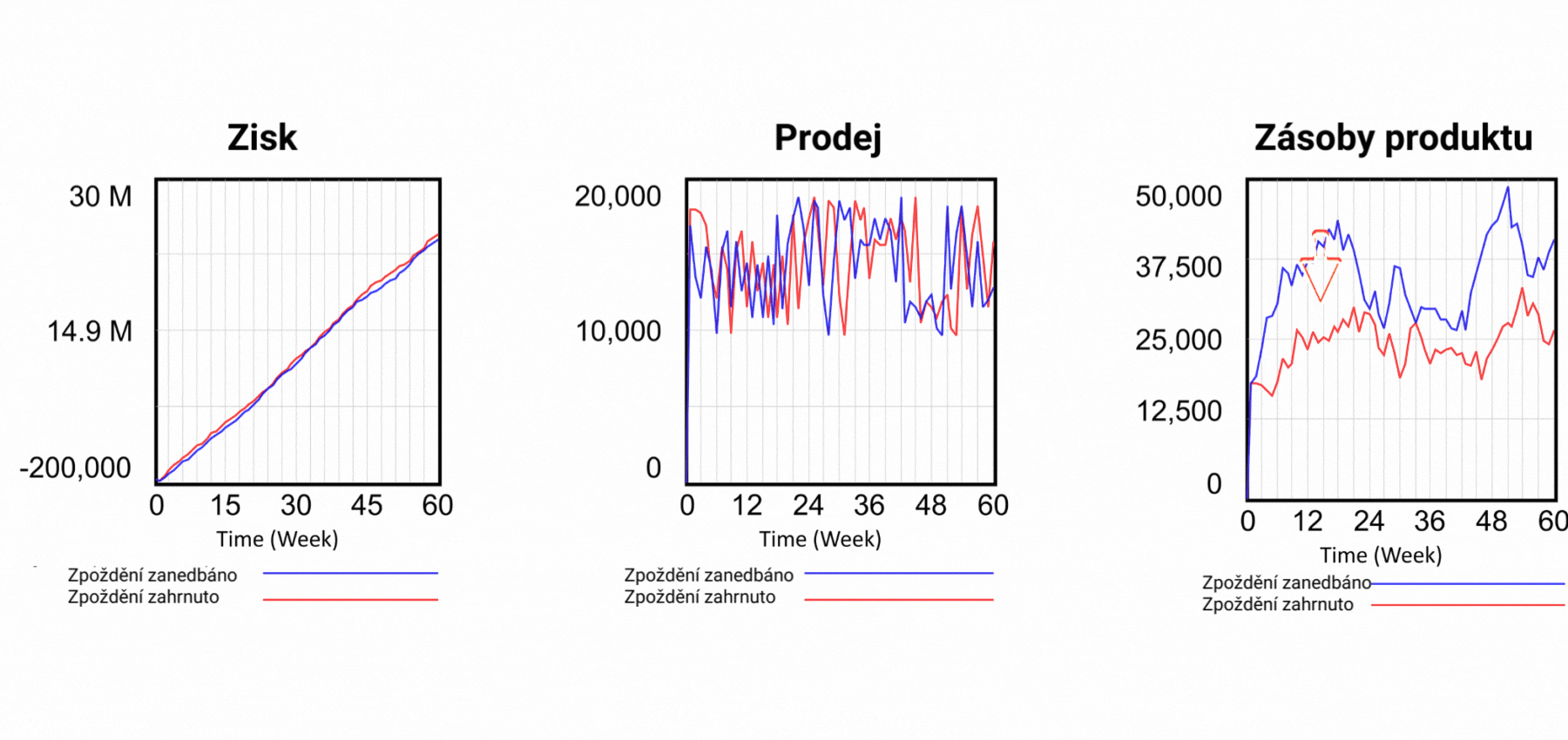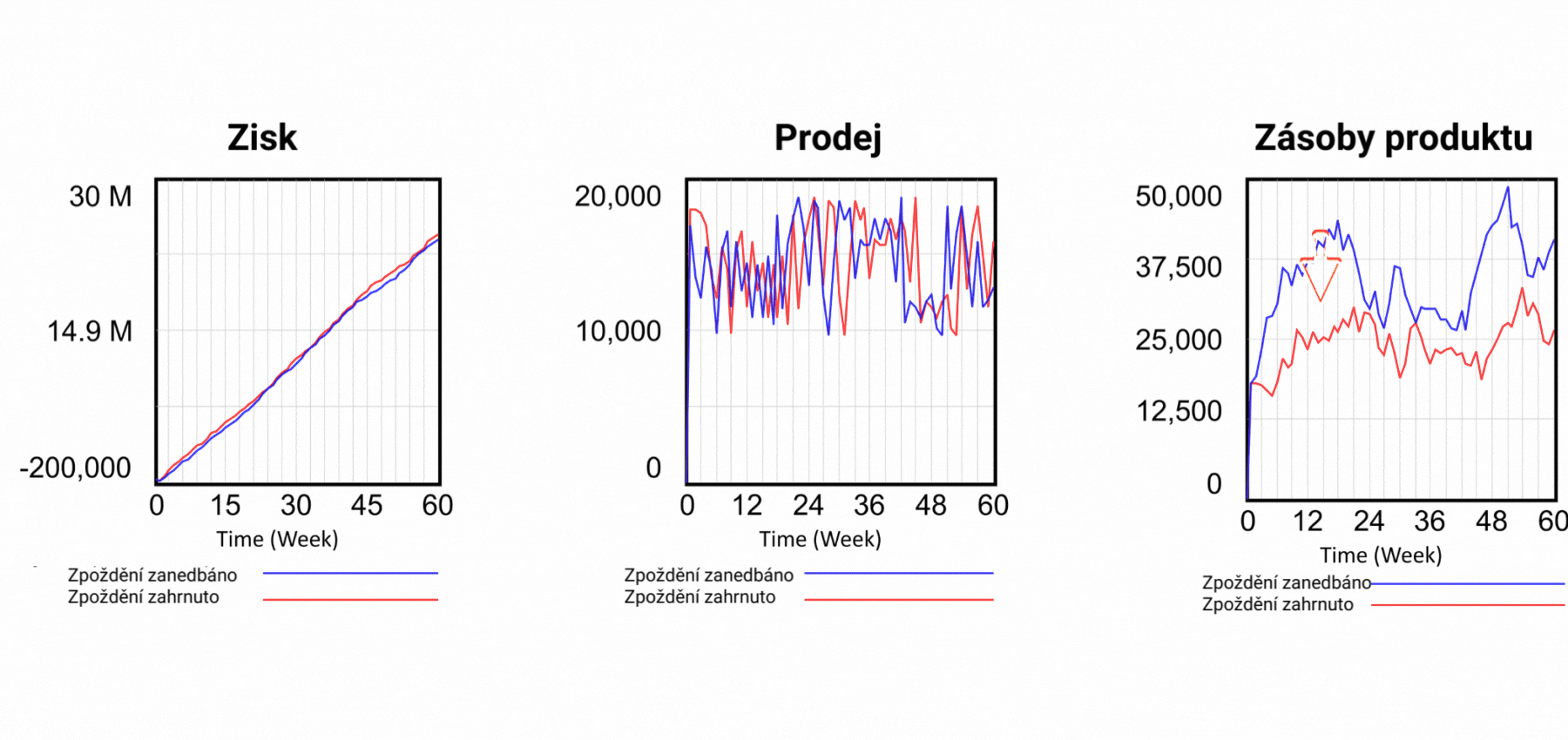
Obrázek 7 Výsledky simulačních scénářů po zohlednění vlivu zpoždění.
Tím však problémy se statickými modely v tabulkách nekončí. Každý, kdo pracuje v reálném světě, ví, že mezi akcí a reakcí je často velmi výrazná prodleva. Například v našem jednoduchém podniku existuje zpoždění mezi zadáním produktů do výroby a jejich umístěním do skladu a mezi objednávkou a dodáním zákazníkovi. Ještě větší zpoždění však existuje mezi investicí do marketingu a jeho účinkem na poptávku. Toto zpoždění se mění v závislosti na rozsahu marketingové kampaně. V systémových diagramech se zpoždění obvykle vyznačuje dvěma na šipku kolmými čarami, jako na obrázku 2 mezi Vlivem marketingu na poptávku a Poptávkou. V našem dynamickém modelu zapojíme dosud neuplatněný marketing a hlavně zavedeme zpoždění výroby o 3 týdny a zpoždění expedice výrobku o 2 týdny, přesně jako ve skutečné firmě, kterou modelujeme. V tabulkových procesorech nelze žádná zpoždění zohlednit, a proto se výsledky počítají, jako by zpoždění neexistovala. Výsledky na obrázku 7 ukazují, že zpoždění ve skutečnosti znamená nižší objem zásob. Představte si, že sestavujete plán na příští rok a v něm počítáte s potřebným kapitálem, který bude o 100 % vyšší než ve skutečnosti. A to jsme ještě nezapočítali zpoždění v dodávkách materiálu, lidských zdrojů, závazků, pohledávek a případných reklamací. Už teď je ale jasné, že schopnost tabulkového procesoru zachytit skutečné chování podniku je ve srovnání s dynamickým modelem mizivá.
Pokud jste dočetli až sem, znamená to, že vás toto téma zajímá a hlavně, že se chcete učit. Zveme vás do našich vzdělávacích programů, naučíme vás vše, co potřebujete k vytvoření modelů schopných zachytit reálné chování podniků, veřejné politiky a vlastně všeho, co se mění v čase. Chcete-li si sami vyzkoušet simulaci a porovnat statické výpočty s dynamickými, prostudujte tento článek. Nezapomeňte se seznámit s naším softwarem a literaturou.